Hello can someone help me in this pls i need it today now PLS i will give 25 points
Answers
Answer:
Look below
Step-by-step explanation:
Convert -8/5 into a decimal
-8/5 = -1 3/5 = -1.6
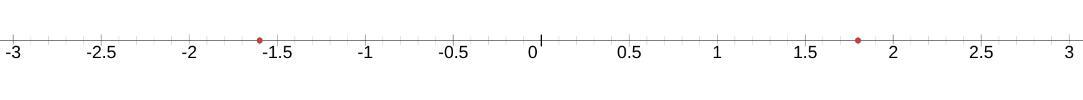
Related Questions
translate the following into an equation:five increased by triple a number results in 52
Answers
Answer:
3n+5=52
Explanation:
• Let the number = n
,• Triple the number = 3n
,• Five increased by triple a number = 3n+5
,• The result is 52.
The equation is:
[tex]3n+5=52[/tex]Fun zone offers four party packages. The prices for each package are $50 more on weekends than they are on weekdays, as shown in the table below
Answers
Okay, here we have this:
Considering the provided information, if the relationship between the number of packages and price is a function, so we obtain the following:
Since a function is a relation where each element of the first set is assigned a single element of the second set or none at all, in this case the first set is the number of the package, and the second the price. However, it does not comply with the requirement that each element of the first set is assigned a single element of the second.
Then, finally we obtain that since the condition is not satisfied, it means that it is not a set. And the correct answer will be the third option.
The diagonals of a parallelogram are 56 in and 34 in and intersect at angle of 120° find the length of the shorter side
Answers
Diagonals of a parallelogram bisect each other.
The opposite sides of a parallelogram are parallel and equal.
In a triangle, the larger angle has a longer opposite side and a smaller angle has a shorter opposite side.
Law of cosine: If a, b, c are three sides of a triangle and A is the angle opposite to the side a, then
[tex]a^2=b^2+c^2-2bc\cos A[/tex]The diagonals of a parallelogram are 56 inches and 34 inches. They bisect each other and form 4 triangles.
Let ABCD is a parallelogram and the diagonals AC and BD intersect each other at point O.
AB parallel to CD , AB=CD.
BC parallel to AD , BC=AD.
Diagonals intersect at an angle of 130 degrees.
m∠AOD=120 degree.
BD is a straight line. So,
m∠AOD+m∠AOB=180 degree
120+m∠AOB=180 degree
∠AOB =180-120=60 degree.
The opposite side of 130∘, (AD and BC) are the longer sides and the opposite side of 60∘, (AB and CD) are the shorter sides.
Use the law of cosine in triangle AOB,
[tex]AB^2=OA^2+OB^2+2(OA)(OB)\cos 60^{\circ}[/tex][tex]AB^2=28^2+17^2+2\times28\times17\cos 60^{\circ}[/tex][tex]AB^2=784+289+476[/tex][tex]AB^2=1549[/tex][tex]AB=39.35\text{ in}[/tex]The length of shorter side is AB =39.35 in.
SHOW THE EQUATION YOU SET UP.91 is what percent of 14?
Answers
1) Given that we want to know how much in percentage is 91 to 14 we can write out:
[tex]\begin{gathered} 14-------100\% \\ 91--------x \\ 14x=9100 \\ \frac{14x}{14}=\frac{9100}{14} \\ x=650\% \end{gathered}[/tex]Note that we crossed multiply that. And since 91 is way over 14, then it is clearly greater than 100%
Thus, 91 corresponds to 650% of 14
Question 9 Which equation would generate the arithmetic sequence: -5,- 14,- 23,-32,-41, A an = -5+9(n-1) B an = -5-9(n-1) C None of the other answers are correct D an = 9+5(n-1) E a = 9-5(n-1)
Answers
B
1) Examining the Arithmetic Sequence:
(-5,-14, -23,-32,-41,..)
We have the following information:
a_1 = -5
Common ratio:-9
2) From these data, we have the Explicit formula:
[tex]a_n=-5_{}-9(n-1)[/tex]3) Looking at the options we have some formulas, so we can state that the equation that would generate the Arithmetic Sequence is described in option B
Noah has a coupon for 30% off at his favorite clothing store can you use it to buy a hoodie and a pair of jeans I paid $28 for the jeans after using the coupon what is the regular price
Answers
Given:
Coupon = 30%
Amount paid after using the coupon = $28
Let's find the regular price.
The coupon is a form of voucher that enables someone to get a discount off a product.
This means after a discount of 30%, the new price of the jeans is $28
Thus, to find the regular price, we have:
[tex]28=P(1-\frac{30}{100})[/tex]Where P represents the regular price.
From the equation above, let's solve for P.
[tex]28=P(1-0.3)[/tex][tex]\begin{gathered} 28=P(0.7) \\ \\ 28=0.7P \\ \\ \text{Divide both sides by 0.7:} \\ \frac{28}{0.7}=\frac{0.7P}{0.7} \\ \\ 40=P \\ \\ P=40 \end{gathered}[/tex]Therefore, the regular price for the Jeans is $40
ANSWER:
$40
By the congruent supplements theorem, what can youconclude?CBG = _DBGO_FBC = _DBG_CBG is supplementary to _DBF._FBC is supplementary to DBG.
Answers
The congruent supplements theorem basically states that if we have two pairs of supplementary angles, say A and B are supplementary and C and D are supplementary and one of angle of each pair are congruent, say A congruent to C, then the other two are also congruent (say B congruent to D)
In our case, the angle A is the angle FBC, B is the angle CBG. C is the angle DBG and D is the angle DBF. Since B is congruent to D then A is congruent to C. So angle FBC is congruent to angle DBG, which is option 2
Helpppppp plas I don’t know the answer and I’m crying
Answers
The given expressions are:
A: 3(x+2)
B: 3x+6
When two expressions are equivalent, it doesn't matter which x-value you use, the result will always be the same, then option C and option D show that these expressions are equivalent, because we will obtain the same result, regardless of the value of x.
Now, the distributive property states:
a(x+y)=a*x+a*y
If we apply this property to expression A, we have:
3*x+3*2=3x+6
Thus, by applying the distributive property we can see that those expressions are equivalent.
The option B which says "Both expressions involve addition" does not show that these expressions are equivalent since we can have different expressions as: 4x+8, x+1, etc... and these are not equivalent.
Thus, the statement which doesn't show that these expressions are equivalent is B. Both expression involve addition..
Now, the
Y is inversely proportional to the cube of x. If Y = 5 when x = 2, then k = 20.
Answers
Answer:
False
Explanation:
Y is inversely proportional to the cube of x. Mathematically, this means
[tex]y\propto\frac{1}{x^3}[/tex]If we now introduce a proportionality constant k, then we get
[tex]y=\frac{k}{x^3}[/tex]Now if y = 5 when x = 2, then
[tex]5=\frac{k}{2^3}[/tex][tex]5=\frac{k}{8}[/tex]Multiplying both sides by 8 gives
[tex]5\times8=k[/tex][tex]\boxed{k=40.}[/tex]Hence, the value of k is NOT 20.
Therefore, the statement that "If Y = 5 when x = 2, then k = 20." is false.
at the time of the weather forecast on Evening News, the temperature was 4 degrees below zero. The temperature continue to fall at a rate of 5 degrees each hour or due to a winter storm. Which equation represents the relationship between the temperature t, in degrees after h hours
Answers
A vacant lot in the shape of a rectangle measures 110 feet by 30 feet A)what is the perimeter of the lot?B)what is the area of the lot?
Answers
SOLUTION
Since the vacant lot has the shape of a rectangle;
A. To measure the perimeter, we will use the formula for perimeter of a rectangle given as
[tex]P=2(l+b)[/tex]Where L is the length and b is the breadth or width
So, the perimeter becomes
[tex]\begin{gathered} P=2(l+b) \\ P=2(110+30) \\ P=2(140) \\ P=2\times140 \\ P=180ft \end{gathered}[/tex]B. The area of a rectangle is given as
[tex]A=l\times b[/tex]So, the area becomes
[tex]\begin{gathered} A=110\times30 \\ A=3300ft^2 \end{gathered}[/tex]Therefore, the Perimeter is 180 feet and the Area is 3300 square-feet.
Find the area of the figure. Use 3.14 for .18 in9 inO A. 97.2 in2O B. 122.24 in2O C. 61.12 in2D. 86.24 in2
Answers
SOLUTION
We want to solve the question below
The figure consists of a semi-circle and a triangle. So the area of the figure becomes
Area of semi-circle + area of triangle
The semi-circle has a diameter of 8 in. So the radius becomes
[tex]r=\frac{diameter}{2}=\frac{8}{2}=4in[/tex]Area of the semi-circle is given as
[tex]\begin{gathered} \frac{1}{2}\times\pi r^2 \\ \frac{1}{2}\times3.14\times4^2 \\ \frac{1}{2}\times3.14\times16 \\ =25.12\text{ in}^2 \end{gathered}[/tex]Area of the triangle is
[tex]\begin{gathered} \frac{1}{2}\times base\times height \\ \frac{1}{2}\times9\times8 \\ 9\times4 \\ =36\text{ in}^2 \end{gathered}[/tex]So Area of the figure becomes
[tex]\begin{gathered} 25.12+36 \\ =61.12\text{ in}^2 \end{gathered}[/tex]Hence the answer is option C
Nina has prepared the following two-column proof below. She is given that ZOLN = ZLNO andShe is trying to prove that ol=on
Answers
First error:
Draw OE as a perpendicular bisector of LN
First correction:
Draw OE as a bisector of By construction
Second error:
By transitive property of equality
x and y are equal because of the property of the sum of the internal angles of a triangle
a + b + x = 180°
a + b + y = 180°
Second correction:
Sum of the internal angles of a triangle
Consider the linear equation 2y - 3x = 5.Are (-1, 1) and (4, 1) solutions to the inequality 2y - 3x < 5? Explain how you know.
Answers
Solution
For this case we have the following inequality:
2y-3x< 5
And we can solve for y like this:
2y < 3x+5
y < 1/2 (3x+5)
We can replace the points and we can verify:
x=-1 y=1/2*(3*-1 +5) = 1/2(-3+5)= 1 then y is not <1
x=4 y=1/2*(3*4 +5) = 1/2(12+5)= 17/2 then y is not <1
A landscaper is designing a flower garden in the shape of a right triangle. She wants 10ft of a perennial border to form the hypotenuse of the triangle, and one leg is to be 2ft longer than the other. Find the lengths of the legs?
Answers
Let the length of one leg be x, then other leg length is (x+2).
Determine the length of leg of triangle by using the pythagoras theorem.
[tex]\begin{gathered} (10)^2=(x)^2+(x+2)^2 \\ 100=x^2+x^2+4x+4 \\ x^2+2x-48=0 \\ x^2+8x-6x-48=0 \\ x(x+8)-6(x+8)=0 \\ (x-6)(x+8)=0 \end{gathered}[/tex]So values of x is 6 and -8. Negative length is not possible. The value of x is 6.
Determine the length of other leg.
[tex]\begin{gathered} x+2=6+2 \\ =8 \end{gathered}[/tex]Thus length of legs of triangle are 6 ft and 8 ft.
Find the area between the graph of y= -12x^3 and the x-axis on the interval [-1, 1]. Write the exact answer. Do not round.
Answers
Recall that the integral of the area between the graph of two functions, in an interval [a,b] is:
[tex]\int ^b_a|f(x)-h(x)|dx\text{.}[/tex]Now, if f(x) is an odd function, we can use the following property:
[tex]\int ^a_{-a}|f(x)|dx=2\int ^a_0|f(x)|dx\text{.}[/tex]Now, notice that the function y=-12x³ is an odd function, therefore:
[tex]\int ^1_{-1}|y-0|dx=2\int ^1_0|-12x^3|dx=2\int ^1_012x^3dx\text{.}[/tex]Applying the linearity of the integral we get:
[tex]24\int ^1_0x^3dx=24\frac{x^4}{4}|^1_0=24(\frac{1}{4}-0)=\frac{24}{4}=6.[/tex]Answer: 6.
Circle describe and correct each error Graph y=x-4 using slop-intercept form.M= -4y-int=1
Answers
Given:
Given that a graph of the function
[tex]\begin{gathered} y=x-4 \\ m=-4 \\ y-int=1 \end{gathered}[/tex]Required:
To find error in the given question.
Explanation:
The standard equation of the line is
[tex]y=mx+c[/tex]Where m slope and c is y-intercept.
Consider the given equation
[tex]y=x-4[/tex]Here the slope is 1 and y-intercept is at -4.
And the graph of the equation is,
Final Answer:
The error is :
[tex]\begin{gathered} m=-4 \\ y-int=1 \end{gathered}[/tex]the graph shows function m, a transformation of f(x) = x^1/2replace a and h to create the equation for function m. (picture of graph listed below)
Answers
Answer:
[tex]\begin{gathered} a\text{ = 2, h = 3} \\ m(x)\text{ =2\lparen x + 3\rparen}^{\frac{1}{2}} \end{gathered}[/tex]Explanation:[tex]\begin{gathered} The\text{ parent function:} \\ f(x)\text{ = x}^{\frac{1}{2}} \\ \\ new\text{ function is given as:} \\ m(x)\text{ = a\lparen x + h\rparen}^{\frac{1}{2}} \\ We\text{ need to find a and h} \end{gathered}[/tex]We need to translate the parent function in order to get the function for m(x).
The first thing we will do is to get the graph of the parent function. Then we will compare with the graph of m(x) to determine the transformation applied to it.
The parent graph starts at the origin (0, 0). But the graph of m(x) starts at -3. This means the graph was translated (moved) 3 units to the left.
When we move to the left, the value will be a positive number when writing the function
So our h = 3
[tex]\text{m\lparen x\rparen= a\lparen x + 3\rparen}^{\frac{1}{2}}[/tex]Next, is to find a:
The value of a could be less than 1, 1 or greater than 1. To determine the value, pick a point from the graph of m(x) given.
Using point (6, 6), we will substitute this value into the translated function to get a
[tex]\begin{gathered} \text{x = 6, y = 6} \\ y\text{ in this case = m\lparen x\rparen} \\ m(x)\text{ = a\lparen x + 3\rparen}^{\frac{1}{2}} \\ 6\text{ = a\lparen6 + 3\rparen}^{\frac{1}{2}} \\ 6\text{ = a\lparen9\rparen}^{\frac{1}{2}} \\ 6\text{ = a\lparen}\sqrt{9}) \\ 6\text{ = a\lparen3\rparen} \\ a\text{ = 6/3 } \\ \text{a = 2} \end{gathered}[/tex]To ascertain we got the right function, I'll plot with the values of h and a we got and compare:
[tex]\begin{gathered} a\text{ = 2, h = 3} \\ m(x)\text{ =2\lparen x + 3\rparen}^{\frac{1}{2}} \end{gathered}[/tex]The graph above is the same as the given one in the question
Where in the xy-plane are the points with x < 0 and y is greater than or equal to 0?*O Quadrant IO Quadrant IIO Quadrant IIIO Quadrant IV
Answers
Answer:
Quadrant II
Explanation:
In the xy-plane:
• The value of x is less than 0 in Quadrant II and Quadrant III.
,• The value of y is greater than or equal to 0 in Quadrant I and Quadrant II.
Therefore, the quadrant with points x < 0 and y≥0 is Quadrant II.
answer in standard form and contain only positive(x+2) (2x^2-x-9)
Answers
(x+2) (2x^2-x-9)
Apply distributive property:
x(2x^2)+x (-x) + x (-9) + 2 (2x^2) + 2 (-x) + 2 (-9)
2x^3 - x^2 - 9x + 4x^2 - 2x - 18
Combine like terms:
2x^3 -x ^2 + 4x^2 - 9x -2x -18
2x^3 + 3x^2 - 11x - 18
Write an equation in standard form of the line passing through the points (12, 6) and (-4, 10).The equation is . (Type your answer in standard form.)
Answers
Answer:
The equation, in the standard form is: x + 4y = 36
Step-by-step explanation:
The standard form of the equation of a line has the following format:
Ax + By = C.
First, I will place the equation of the line in slope-intercept formula, which is:
y = ax + b. Then, I pass to the standard.
Passes through the point (12,6):
This means that when x = 12, y = 6.
So
y = ax + b
6 = 12a + b
b = 6 - 12a
Passes through the point (-4,10):
This means that when x = -4, y = 10. SO
10 = -4a + b
Since b = 6 - 12a
10 = -4a + (6 - 12a)
10 = -4a + 6 - 12a
10 - 6 = -4a - 12a
-16a = 4
16a = -4
a = -4/16
Simplifying by 4
a = -1/4
b = 6 - 12a = 6 - 12*(-1/4) = 6 + 3 = 9
So
y = ax + b
y = -(x/4) + 9
(x/4) + y = 9
Multiplying everything by 4
x + 4y = 36
The equation, in the standard form is: x + 4y = 36
a man filled his car's 16 galllon gas tank. he took a trip and used 1/2 of the gas. how many gallons of gas were used?
Answers
Given:
The capacity of the gas tank = 16 gallon
He filled the gas tank and used half of it for a trip i.e
fraction of gallon used = 1/2
Solution
The gallon of gas used can be calculated using the formula:
[tex]\text{gallon of gas used = fraction of gallon used }\times\text{ gallon of gas filled}[/tex]Substituting, we have:
[tex]\begin{gathered} \text{gallon of gas used = }\frac{1}{2}\text{ }\times\text{ 16} \\ =\text{ 8 gallons} \end{gathered}[/tex]Answer: 8 gallo
On October 23, 2011, one U.S. dollar was worth 13.65 Mexican pesos.(a) On that date, how many pesos was 81.35 dollars worth?Round your answer to the nearest hundredth of a peso.pesos(b) On that date, how many dollars was 91.03 pesos worth?Round your answer to the nearest hundredth of a dollar.
Answers
Solution
We are given that
[tex]\text{ \$}1=13.65\text{ }pesos[/tex]a.
[tex]\begin{gathered} \text{ \$}81.35=81.35\times13.65\text{ }pesos \\ \\ \text{ \$}81.35=1110.43\text{ }pesos\text{ \lparen to the nearest hundredth\rparen} \end{gathered}[/tex]b.
[tex]\begin{gathered} 1\text{ }pesos=\text{ \$}\frac{1}{13.65} \\ \\ 91.03pesos=\text{ \$}\frac{1}{13.65}\times91.03 \\ \\ 91.03pesos=\text{ \$}6.67\text{ \lparen to the nearest hundredth\rparen} \end{gathered}[/tex]A farmer has 1776 feet of fencing available to enclose a rectangular area bordering a river. If no fencing is required along the river, find the dimensions of the fenced area that will maximize the area. What is the maximum area?
Answers
As per the given perimeter of the rectangular area, the maximum area without fencing is 788544 square feet.
Perimeter of rectangle
Perimeter of the rectangle is defined as the total length or distance around the boundary of a rectangle.
And the formula that is used to measure the perimeter of the rectangle is
P = L x B
Where
L refers the length
B refers the breadth
Given,
A farmer has 1776 feet of fencing available to enclose a rectangular area bordering a river.
Here we need to find if no fencing is required along the river, then what will be the dimensions of the fenced area that will maximize the area.
Let us consider L and W be the length and width of the rectangular respectively.
And also, let the river run along L.
So, the perimeter to be covered by fence is written as,
=> P = L + 2W.
Therefore, when we apply the value of perimeter in it, then we get,
=> 1776 =L + 2W
Here we need the value of L, so, the equation is rewritten as,
=> L = 1776 - 2W
Now, we have to apply these value on the area formula, then we get,
A = (1776-2W) x W
When we simplify it, then we get,
=> A = 2700W-2W²
This is in the form of quadratic equation.
So, let us assume that the vertex of the rectangular at maximum area will give maximum width.
Then it can be obtained as, (W,A),
where the value of
W = -b/2a
Here the value of b = 1776 and a = -2
By applying these values on the formula, then we get the value of W as,
=> W = -1776/2*(-2)
=> W = -1776/-4
=> W = 444ft.
Therefore, the length is
=> L = 1776 - 2(444)
=> L = 1776 - 888
=> L = 888
Maximum area, A=888*888 = 788544 square feet.
To know more about Perimeter of the rectangle here.
https://brainly.com/question/15287805
#SPJ1
Help on any of these problems would be appreciated. Thanks! Question 1
Answers
Theorem: The measure of the angle at the center is equal to the measure of the angle at the circumference.
Hence, the answer is
[tex]x=70^0[/tex]For an equation with fractions,why is it helpful to multiply both sides of theequation by the LCD?
Answers
When you multiply both sides of an equation with fractions with the lowest common denominator, it simplifies the equation, so that adding/subtracting/multiplying and or dividing makes it easier.
Suppose that y varies directly with x and y = 2 when x =16 write a direct variation equation that relates x and y
Answers
The equation of the direct variation is expressed as: y = 1/8x.
How to Write a Direct Variation Equation?The equation of a direct variation between two variables, say x and y, is expressed as y = kx, where k is the constant of proportionality, if y varies directly as x.
Therefore, substitute y = 2 and x = 16 into y = kx to find the value of k:
2 = k(16)
Divide both sides by 16
2/16 = k
1/8 = k
k = 1/8.
To write the equation of the direct variation, substitute k = 1/8 into y = kx:
y = 1/8x.
Learn more about equation of direct variation on:
https://brainly.com/question/6499629
#SPJ1
f(x) = 6x^4 + 6Use the limit process to find the slope of the line tangent to the graph of f at x = 2. Slope at x= 2:__Find an equation of the line tangent to the graph of f at x = 2:__
Answers
The given function is
f(x) = 6x^4 + 6
The formula for the limit is shown below
[tex]\begin{gathered} f^{\prime}(x)\text{ = }\lim _{h\to0}\text{ }\frac{f(x\text{ + h) - f(x)}}{h} \\ \text{Substituting x = x + h into the function, we have} \\ f^{\prime}(x)\text{ = }\lim _{h\to0}\text{ }\frac{6(x+h)^4+6-(6x^4+6)}{h} \\ f^{\prime}(x)\text{ = }\lim _{h\to0}\text{ }\frac{6(h^4+4h^3x+6h^2x^2+4hx^3+x^4)+6-6x^4-6}{h} \\ f^{\prime}(x)\text{ = }\lim _{h\to0}\text{ }\frac{6h^4+24h^3x+36h^2x^2+24hx^3+6x^{4\text{ }}-6x^4\text{ + 6 - 6}}{h} \\ f^{\prime}(x)\text{ = }\lim _{h\to0}\text{ }\frac{h(6h^3+24h^2x+36hx^2+24x^3)}{h} \\ h\text{ cancels out} \\ \end{gathered}[/tex]Evaluating the limit at h = 0, we would substitute h = 0 into 6h^3 + 24h^2x + 36hx^2 + 24x^3
It becomes
6(0)^3 + 24(0)^2x + 36(0)x^2 + 24x^3
The derivative is 24x^3
f'(x) = 24x^3
This is the slope of the tangent line is at x = 2
By substituting x = 2 into f'(x) = 24x^3, it becomes
f'(2) = 24(2)^3 = 192
To find the y coordinate of the point, we would substitute x = 2 into
f(x) = 6x^4 + 6
y = 6(2)^4 + 6 = 102
Thus, the x and y coordinates are (2, 102) and the slope is 192
The equation of the line in the point slope form is
y - y1 = m(x - x1)
Thus, the equation of the tangent is
y - 102 = 192(x - 2)
Reasoning Krishan wants his quiz average to be at least90 so that he can get an A in the class. His current quiz scoresare: 80, 100, 85. What does he have to get on his 2052next quiz to have an average of 90?A 85B 90C 92D 95
Answers
Average = total of all test scores/number of tests
90 = ( 80 + 100 + 85 + x ) / 4
Solve for x
90 (4) = 80 + 100 +85 + x
360 = 265 + x
360-265 = x
95 = x
How many degrees would this octagon need to be rotated clockwise around its center to get point K to point G
Answers
In the image below you can observe that we have to rotate four times.
Where each rotation is 45 degrees. So,
[tex]45\times4=180[/tex]Hence, the right answer is A. 180°.