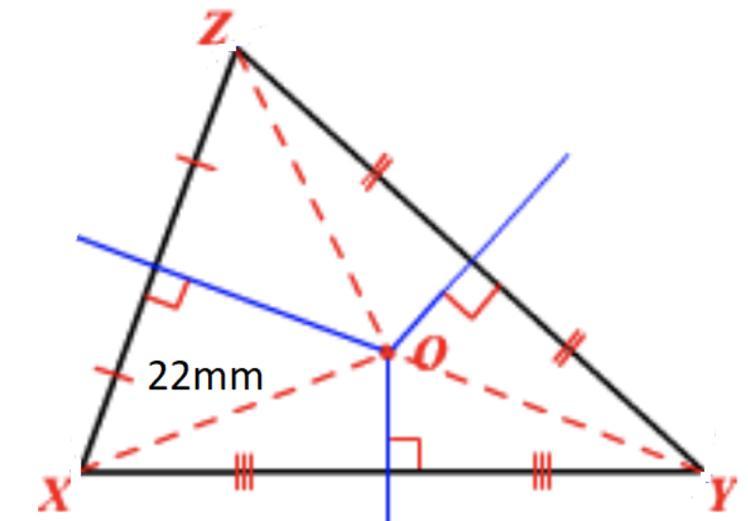
Given Triangle XYZ, with Circumcenter O. If the distance from XO is 22mm. What is the distance of both YO and ZO?Required to answer. Single choice. 182022241313,
Answers
Solution
Circumcenter Theorem
The vertices of a triangle are equidistant from the circumcenter.
The perpendicular bisectors intersect in a point and that point is equidistant from the vertices.
Any point on the perpendicular bisector of a segment is equidistant from the endpoints of the segment.
Therefore, YO and ZO is 22mm( By the transitive property)
Related Questions
Quality control finds on average that 0.026% of the items from a certain factory are detective. One month, 4000 items are checked. How many items are expected to be detective?
Answers
Given that 4000 items are checked in one month, let the number of detective items be represented as y.
Quality control finds on average that 0.026% of the items in the factory are detective. This implies that
[tex]\text{Number of }\det ective\text{ items = }\frac{\text{0.026}}{100}\times\text{Total number of items checked}[/tex]When 4000 items are checked, we have the number of detective items to be evaluated as
[tex]\begin{gathered} \text{Number of }\det ective\text{ items = }\frac{\text{0.026}}{100}\times\text{Total number of items checked} \\ y=\frac{0.026}{100}\times4000 \\ \Rightarrow y=1.04 \end{gathered}[/tex]Hence, the number of detective items is 1.04.
You're going to the mall with your friendsand you have $200 to spend from yourrecent birthday money. You discover astore that has all jeans for $25 and alldresses for $50. You really, really want totake home 6 items of clothing because you"need" that many new things. How manypairs of jeans and how many dresses youcan buy so you use the whole $200 (taxnot included)?
Answers
Given that:
- You have $200 to spend.
- The store sells all jeans for $25 and all dresses for $50.
- You want to take home 6 items of clothing.
Let be "j" the number of jeans and "d" the number of dresses you can buy so you use the whole $200 (not including the tax).
Set up this System of Equations using the data provided in the exercise:
[tex]\begin{cases}j+d=6{} \\ 25j+50d={200}\end{cases}[/tex]You can follow these steps in order to solve the System of Equations using the Elimination Method:
1. You can multiply the first equation by -25:
[tex]\begin{cases}-25j-25d={-150} \\ 25j+50d={200}\end{cases}[/tex]2. Add the equations:
[tex]\begin{gathered} \begin{cases}-25j-25d={-150} \\ 25j+50d={200}\end{cases} \\ ------------ \\ 0j+25d=50 \\ 25d=50 \end{gathered}[/tex]3. Solve for "d":
[tex]\begin{gathered} d=\frac{50}{25} \\ \\ d=2 \end{gathered}[/tex]4. Substitute the value of "d" into the first original equation and solve for "j":
[tex]\begin{gathered} j+(2)=6 \\ j=6-2 \\ j=4 \end{gathered}[/tex]Hence, the answer is: You can buy 2 dresses and 4 jeans.
The data points show the amount of money y (in dollars) in an account after a time x (in years).Each figure has the same data points.However, each figure has a different curve fitting the data.The equation for each curve is also shown.Answer the questions that follow.
Answers
SOLUTION
(a) From the slope of the graph, we can see that this is an exponential function
So, the function that best fits the graph is
[tex]y=601(1.05)^x[/tex]Hence the answer to (a) is Figure 1
(b) From the graph of the function we selected, where y represents the amount of money and x the number of years. To get the amount of money, we will substitute x for 18 into the quatiomn, we have
[tex]\begin{gathered} y=601(1.05)^x \\ y=601(1.05)^{18} \\ y=601\times2.406619234 \\ y=1,446.378159448 \end{gathered}[/tex]Hence the answer is $1,446.38
here is a raffle with 500 tickets. One ticket will win a $960 prize, and the rest will win nothing. If you ave a ticket, what is the expected payoff?
Answers
The expected value is a measure of what you should expect to win per game in the long run. Divide the total prize over the number of tickets to find the expected payoff:
[tex]\frac{960}{500}=1.92[/tex]Therefore, the expected payoff is:
[tex]1.92[/tex]As the Earth revolves around the sun, it travels at a speed of approximately 18 miles per second. Convert this speed to kilometers per second. At this speed, how many kilometers will the Earth travel in 15 seconds? In your computations, assume that 1 mile is equal to 1.6 kilometers. Do not round your answers.
Speed:
Distance traveled in 15 seconds
Answers
The speed in kilometers per second is 28.8 kilometers per second
The distance traveled in 15 seconds is 432 kilometers
Converting speed to kilometers per second and distanceFrom the question, we are to convert the speed to kilometers per second
From the given information,
The speed of the Earth is approximately 18 miles per second
Now, we will convert 18 miles to kilometers
Also, from the given information,
We are to assume that 1 mile is equal to 1.6 kilometers
If 1 mile = 1.6 kilometers
Then,
18 miles = 18 × 1.6 kilometers
= 28.8 kilometers
Thus,
The speed is 28.8 kilometers per second
To determine how many kilometers the Earth would travel in 15 seconds
The distance the Earth will travel in 15 seconds = 15 × 28.8
The distance the Earth will travel in 15 seconds = 432 kilometers
Hence, the distance is 432 kilometers
Learn more on Converting speed here: https://brainly.com/question/2681210
#SPJ1
AN ELECTRIC COMPANY MAKES TWO KINDS OF ELECTRIC RANGES- A STANDARD MODEL WHICH YEILDS A $50.00 PROFIT AND A DELUX THAT YEILDS A $60 PROFIT THE COMPANY CAN PRODUCE UP TO 400 DELUXE RANGES AND 500 STANDARD RANGES PER MONTH BUT BECAUSE OF THE MAN HOUR LIMITATIONS THE COMPANY CAN PRODUCE A COMBINED TOTAL OF NOMORE THEAN 600 RANGES PER MONTH. HOW MANY OF EACH TYPE RANGE SHOULD THE COMPANY PRODUCE PER MONTH TO MAX PROFIT? X= THE # OF THE STANDARD RANGES Y= THE # OF DELUXE RANGESA. THE OBJECTIVE FUNCTION IS:B.THE CONSTRAINTS ARE:
Answers
Explanation:
The number of standard ranges is represented as
[tex]x[/tex]The number of delux ranges is represented as
[tex]y[/tex]Hence,
The objective constraint will be
[tex]P=50X+60Y[/tex]The constraints will be given below as
[tex]\begin{gathered} 0\leq X\leq500 \\ 0\leq Y\leq400 \\ X+Y\leq600 \end{gathered}[/tex]00What is the length of BC?17А A9 units11 unitsO 15 unitsO 16 units8С
Answers
ANSWER:
15 units
STEP-BY-STEP EXPLANATION:
We can determine the BC value we can determine it by means of the Pythagorean theorem, with the hypotenuse 17 and the other side 8, therefore:
[tex]\begin{gathered} h^2=a^2+b^2 \\ \\ \text{ We replacing} \\ \\ 17^2=8^2+b^2 \\ \\ b^2=289-64 \\ \\ b=\sqrt{225} \\ \\ b=15 \end{gathered}[/tex]Therefore, the length of BC is 15 units.
Is the vertex of the quadratic function below a maximum or minimum?
Answers
A quadratic equation is of the form below:
[tex]ax^2+bx+c=y[/tex]The vertex of the quadratic equation is the value of y where the curve cut the y-axis.
To find the vertex, we would first first find the x-coordinate of the equation using
[tex]x=-\frac{b}{2a}[/tex]To find the vertex, we would substitute for x in the equation to get y.
Given the quadratic function below
[tex]f(x)=-3x^2-4x+7[/tex]It can be observed that
[tex]a=-3;b=-4,c=7[/tex]The x-coordinate of the vertex is as shown below:
[tex]\begin{gathered} x=-\frac{b}{2a} \\ x=\frac{--4}{2(-3)} \\ x=\frac{4}{-6} \\ x=-\frac{2}{3} \end{gathered}[/tex]The vertex would be
[tex]\begin{gathered} f(-\frac{2}{3})=-3(-\frac{2}{3})^2-4(-\frac{2}{3})+7 \\ f(-\frac{2}{3})=-3(\frac{4}{9})+\frac{8}{3}+7 \\ f(-\frac{2}{3})=-\frac{4}{3}+\frac{8}{3}+7 \\ f(-\frac{2}{3})=\frac{-4+8}{3}+7 \\ f(-\frac{2}{3})=\frac{4}{3}+7 \\ f(-\frac{2}{3})=1\frac{1}{3}+7=8\frac{1}{3}=\frac{25}{3} \end{gathered}[/tex]Hence, the vertex of the quadratic function is (-2/3,25/3)
It should be noted that when a is positive, the quadratic graph opens upward and the vertex is minimum but when a is negative, the quadratic curve opens downward, and the vertex would be maximum
The graph of the quafratic function given is shown below
It can be observed that the vertex is maximum
which is the graph of f(x) and the translation g(x)=f(x+1)
Answers
SOLUTION
Step 1 ;
In this question, we are meant to examine the graph of the function,
[tex]f\text{ ( x ) = 3 sin ( }\frac{1}{2}\text{ x )}[/tex]We also to know the sketch of the graph of f ( x ) and
the translation y ( x ) = f ( x + 1 )
Step 2 :
The graph is as shown below:
CONCLUSION: OPTION A IS VERY CORRECT.
A patient that you are tending to cannot exceed 500 Cal per meal. You notice that on the label the meal has 21grams of fat, 68 grams of carbohydrates, and 40 grams of protein. On average fat has 9 Cal/g, carbohydrates have4 Cal/g, and protein has 4 Cal/g.a) How much energy would the patient consume if they would eat the whole meal?b) What is the unit symbol of the answer?c) Are they within the 500 Cal limit? Input Y for yes and N for no
Answers
To determine the total amount of calories consumed in that meal, we have to multiply the number of grams of each type of nutrient by the energy provided by each gram of that nutrient.
We are given that 1 gram of fat has 9 calories, therefore, 21 grams of fat have:
[tex]9\times21\text{ calories=189 calories}[/tex]1 gram of carbohydrates gives 4 calories of energy, therefore, 68 grams have
[tex]68\times4\text{ calories= }272\text{ calories.}[/tex]1 gram of protein has 4 calories, therefore, 40 grams of protein has:
[tex]40\times4\text{ calories=160 calories.}[/tex]The mean has a total of:
[tex](189+272+160)\text{ calories=621 calories.}[/tex]Answer:
A) 621 Cal.
B) Cal.
C) N.
Question 1 Given a mean of 25 and a standard deviation of 2.5, what is the z-score of a data value X = 29? -1.06 1.6 ООО -1.6 1.06
Answers
The information we have is:
Mean:
[tex]\mu=25[/tex]Standard deviation:
[tex]\sigma=2.5[/tex]Value of x:
[tex]x=29[/tex]--------------------------------------------------------
To solve this problem, we need to use the z-score formula:
[tex]z=\frac{x-\mu}{\sigma}[/tex]Substituting our values:
[tex]z=\frac{29-25}{2.5}[/tex]We need to solve the subtraction first:
[tex]z=\frac{4}{2.5}[/tex]Finally, solve the division to find the z-score:
[tex]z=1.6[/tex]the z-score is 1.6
Answer: 1.6
Write an equation for the line parallel to the given line that contains C. C(4,7); y = - 2x + 1 (Type your answer in slope-intercept form.)
Answers
Let's begin by listing out the given information:
Equation of line: y = -2x + 1
Point C (x, y) = (4, 7)
[tex]y=-2x+1\Rightarrow m=-2[/tex]Parallel lines have the same slope. As such, the slope of the parallel line must also be -2
Using point slope equation of a straight line, we have:
[tex]\begin{gathered} y-y_1=-2\left(x-x_1\right) \\ at(x,y)=(4,7) \\ y-7=-2(x-4) \\ y-7=-2x+8 \\ y=-2x+8+7 \\ y=-2x+15 \end{gathered}[/tex]Graph the given functions, fand g, in the same rectangular coordinate system Select integers for x, starting with-2 and ending with 2, and describe how the graph of g is related to the graph off.f(x)=x?_g(x)=x² - 3
Answers
Given
The functions,
[tex]\begin{gathered} f(x)=x^2 \\ g(x)=x^2-3 \end{gathered}[/tex]To complete the ordered pairs for f(x)=x².
Explanation:
It is given that,
[tex]\begin{gathered} f(x)=x^2 \\ g(x)=x^2-3 \end{gathered}[/tex]That implies, for x=-2,
[tex]\begin{gathered} f(-2)=(-2)^2 \\ =4 \end{gathered}[/tex]Also, for x=-1.
[tex]\begin{gathered} f(-1)=(-1)^2 \\ =1 \end{gathered}[/tex]For x=0,
[tex]\begin{gathered} f(0)=0^2 \\ =0 \end{gathered}[/tex]For x=1,
[tex]\begin{gathered} f(1)=1^2 \\ =1 \end{gathered}[/tex]For x=2,
[tex]\begin{gathered} f(2)=2^2 \\ =4 \end{gathered}[/tex]Hence, the ordered pairs are,
[tex]\left(-2,4\right),(-1,1),(0,0),(1,1),(1,4).[/tex]What is the equation of a line that passes through the point (8, -4) and is parrallel to the line 6x + 2y = 9
Answers
Answer:
the answer Is y= -3x +20.
Anylu drew a picture of her bedroom using the scale 1in=2ft. In her drawing the length of her bedroom was 3 1/2 ftand the width of her room was 3 1/8 in. What are the actual dimensions of her room?Ready? Enter your answer here.
Answers
Answer: 7 ft x 6.25 ft
Explanation:
To answer this question we need to make use of the scale:
[tex]1in=2ft[/tex]This means that 1 inch of her drawing represents 2 feets in real life.
To convert from the measurements of her drawing to the actual measurements of her room we need to take the quantity in inches and multily it by 2 and now they become feet.
Length of the room
In her drawing: 3 1/2 in
In real life:
[tex]3\frac{1}{2}(2)=3.5(2)=7ft[/tex]Width of the room: 3 1/8 in
In real life:
[tex]3\frac{1}{8}(2)=3.125(2)=6.25ft[/tex]The dimensions of the room are: 7 ft x 6.25 ft
If O is an angle in standard position and its terminal side passes through the point(-15,-8), find the exact value of tan 0 in simplest radical form.
Answers
The definition of the tangent function for a angle in standard form is given by:
[tex]\tan \theta=\frac{y}{x}[/tex]where x and y are the coordinates of the terminal point (x,y).
Then in this case we have:
[tex]\tan \theta=\frac{8}{15}[/tex]Use the following sample Epworth Sleepiness Scores for the problems below;6, 4, 3, 5, 4, 2, 4, 5, 4, 6, 1, 4, 5, 2Sample variance=Sample Standard Deviation=
Answers
Given:
The data are,
[tex]6,4,3,5,4,2,4,5,4,6,1,4,5,2[/tex]To find:
Sample variance and the Sample Standard Deviation
Explanation:
Using the formula,
Solve for the variable x in the equation x + 15 = 62. Question 20 options: A) 47 B) –47 C) 77 D) –77
Answers
Answer:
A) 47
Step-by-step explanation:
x + 15 = 62
x + 15 -15 = 62 -15
x = 47
I’ll give branniest to answer
with work shown
The equation is y=8.52x+6.0 estimate the value of y when x=25
Answers
Answer:
y = 219
Step-by-step explanation:
y = 8.52x + 6.0 ← substitute x = 25
y = (8.52 × 25) + 6.0 = 213 + 6 = 219
Answer:
Y= 219 when x =25
Step-by-step explanation:
Substitute for x = 25
Y= 8.52(25) +6.0
=213 +6
=219
What is the spread of the data? 17 18 19 20 21 22 23 24 25 26 Age of female U.S. Olympic swimmers (years) O A. 21 to 25 years B. 15 to 30 years C. 18 to 25 years O D. 18 to 21 years
Answers
The spread of data is the difference between the maximum value and the minimum value.
Minimum value = 18
Maximum value = 25
Correct option: C . 18 to 25 years
-18. Graph the functions Y, = 0.6* and Y, = 0.3.4 on a graphing calculator.Use a viewing window from -5 to 5 for x and from –2 to 8 for y, witha scale of 1 for both. Sketch the curves.How does the graph of Y, compare with the graph of Y ? Discuss howthe graphs rise or fall and the y-intercepts.
Answers
The Solution:
The given functions are:
[tex]\begin{gathered} y_1=0.6^x \\ y_2=0.3^x \\ \text{for } \\ -5\leq x\leq5,-2\leq y\leq8 \end{gathered}[/tex]From the graphing calculator, we have
Comparing the two graphs:
Both graphs are decreasing simultaneously and rises together. But
[tex]\begin{gathered} y_2=0.3^x\text{ is decreasing faster than } \\ y_1=0.6^x\text{ when decaying. But rises faster when increasing.} \end{gathered}[/tex]They both have the same intercept at point (0,1)
an architect designed a mountain lodge with special viewing windows on the top floor. how many square yards of glass will it take to make in large window?
Answers
Explanation
to find the area of the glass, we can divide the shape into 2 more known shapes, a triangle and a rectangle
so
total area= area of the rectangle(green)+area of the triangle(yellow)
the area of a rectagle is given by:
[tex]\text{Area}_{rectangle}=base\cdot heigth[/tex]and for the triangle, the area is
[tex]\text{Area}_{triangle}=\frac{1}{2}base\cdot height[/tex]then replace
[tex]\begin{gathered} \text{total area=(2 yd }\cdot1\text{ yd)+}\frac{\text{(2 yd }\cdot\text{ 2 yd)}}{2} \\ \text{total area=2 yd}^2+2yd^2 \\ \text{total area=}4yd^2 \end{gathered}[/tex]so, the answer is
[tex]4yd^2[/tex]I hope this helps you
Identify whether the problem is "Sum of Two Cubes" or "Difference of Cubes". Then, factor the problem.x^3 - 8
Answers
We have in this case the difference of Perfect Cubes since we have:
[tex]x^3-8=x^3-2^3[/tex]We know that this case can be factored as follows:
[tex]a^3-b^3=(a-b)\cdot(a^2+ab+b^2)[/tex]If we have that:
a = x
b = 2
Then, we have:
[tex](x-2)\cdot(x^2_{}+2x+2^2)=(x-2)\cdot(x^2+2x+4)[/tex]Therefore, the factored form of the perfect cube (for difference) is:
[tex]undefined[/tex]A small business owner is determining her profit for one month. Her expenses were$230.21 for utilities, $2,679.82 for rent, and $3,975.00 for employee salaries. Shehad $11,449.27 in sales for the month. What is her profit?a. $4,550.00b. $4,564.24C. $4,794.45d. $5,034.66
Answers
Answer:
B) $4,564.24
Explanation:
We are given the following information:
Expenses:
Utilities = $230.21
Rent = $2,679.82
Employee Salaries = $3,975.00
Sales = $11,449.27
The profit is obtained by the difference between Sales and Expenses as shown below:
[tex]\begin{gathered} Profit=Sales-Expenses \\ Profit=11,449.27-(230.21+2,679.82+3,975.00) \\ Profit=11,449.27-6885.03 \\ Profit=4564.24 \\ \\ \therefore Profit=\text{\$}4564.24\text{ } \end{gathered}[/tex]Therefore, the correct option is B
For a function f(x), you know that f(3) = -8 and f(4) = 3. One zero of f(x) would be located between x= and x=
Answers
Problem Statement
The question tells us that f(3) = -8 and f(4) = 3 and we are asked to find where one of the zeros of the function.
Solution
The function f(x) moves from negative to positive when moves from x = 3 to x = 4. This means that the value of f(x) must cross the x-axis between these two values of x.
Answer
Thus, one zero of the function lies between X = 3 and X = 4
4) Which of the following numbers is an integer?- 9.1,-10,20/3
Answers
Given:
[tex]-9.1,-10,\frac{20}{3}[/tex]-10 is an integer.
How many units the function y = |x + 7| is translated from the parent function?Moved 7 units left from the originMoved 7 units right from the originMoved 7 units upwards from the originMoved 7 units downwards from the origin
Answers
According to the given information, the correct answer is the first choice Moved 7 units left from the origin.
The parent function would be |x|, and if we have |x+7| all the function values will be moved 7 units left from the origin.
Marko originally filled out 8 more applications than Henry. Then each boy filled out 3 additional applications, bringing the total to 28. How many applications did each boy originally fill out?Let m= number of applications Marko originally filled outLet h= number of applications Henry originally filled outWhat equation can we make to represent the relationship between the number of applications Marko and Henry originally filled out? AnswerUse your relationship from the question above to create an equation representing the number of applications after completing 3 more each: AnswerThe equation we can use to find the number of applications Henry and Marko each completed is :AnswerThe number of applications Marko originally filled out is AnswerThe number of applications Henry originally filled out is Answer
Answers
We have the next information
m= number of applicantios Marko originally filled out
h= number of applications Henry originally filled out
We know that Marko originally filled out 8 more applications than Henry
m=h+8
Then each filled out 3 additional applications
m+h+6=28
Already we have a system of equations of two variables
For the question What equation can we make to represent the relationship between the number of applications Marko and Henry originally filled out.
m=h+8
Use your relationship from the equation above to create an equation representing the number of applications after completing 3 more each
(h+8)+h+6=28
The equation we can use to find the number of applications Henry and Marko each completed is
2h+14=28
We can solve the equation above
2h=28-14
2h=14
h=14/2
h=7
m=h+8=15
The number of applications Marko originally filled out is 15
The number of applications Henry originally filled out is 7
Can someone help me I’ve been stuck on this for like hours now
Answers
We are given the inequality p>4
We want to find any numbers greater than 4
Any negative numbers are less than 4
1, or any numbers starting with 3 are less than 4
4 is equal to 4
Numbers greater than 4
4.001
4.01
4.1
5
7
9
12
Thomas wants to invite Madeline to a party. He has 80% chance of bumping into her at school. Otherwise, he'll call her on the phone. If he talks to her at school, he's 90% likely to ask her to the party. What is the probability of Thomas inviting Madeline to the party over the phone?
Answers
Recall that the probability must add 1, therefore:
[tex]0.6+x=1[/tex]Solving for x, we get:
[tex]\begin{gathered} x=1-0.6 \\ x=0.4 \end{gathered}[/tex]Therefore, the probability of Thomas inviting Madeline to the party over the phone is:
[tex]0.2\cdot0.4=0.08[/tex]or 8%.