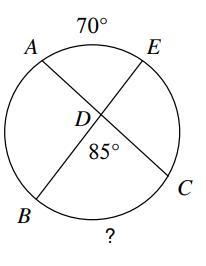
Answers
Let the measure of arc [tex]BC[/tex] be [tex]\alpha[/tex].
[tex]\frac{70+\alpha}{2}=85 \\ \\ 70+\alpha=170 \\ \\ \alpha=\boxed{100^{\circ}}[/tex]
Related Questions
At the pediatrician's office, patients are able to draw a toy from the toy bin. The toy bin has 12 puzzles, 16boxes of crayons, and 2 bouncy balls. What is the probability of drawing...a box of crayons?a puzzle?anything but a bouncy ball?(write your answer as a fraction in lowest terms)
Answers
SOLUTION
Total outcomes = 12 puzzles + 16 boxes of crayons + 2 bouncy balls = 30.
[tex]\begin{gathered} \text{Probability = }\frac{required\text{ outcome}}{\text{total outcome}} \\ \\ \text{probability of drawing a box of crayons = }\frac{16}{30}=\text{ }\frac{8}{15} \end{gathered}[/tex][tex]\text{Probability of drawing a puzzle = }\frac{12}{30}\text{ = }\frac{2}{5}[/tex]Probability of anything but bouncy ball means the probability of drawing out a box of crayons or probability of drawing out a puzzle.
[tex]\begin{gathered} \text{This becomes = }\frac{8}{15}+\frac{2}{5} \\ \\ =\text{ }\frac{8+6}{15}\text{ = }\frac{14}{15} \\ \end{gathered}[/tex]3/8 / 1/4 as a model
Answers
The given expression :
[tex]\frac{3}{8}\div\frac{1}{4}[/tex]Simplify :
I don’t really need an explanation I just need the answers if you could help me out that would be nice
Answers
A' = (3, -1)
B' = (0 -3)
C' = (2, -4)
Explanation:Given:
A = (1, -3)
B = (3, 0)
C = (4, -2)
First we will apply the 90 degrees counterclockwise rotation:
interchange x and y, then negate the new x value
[tex]\begin{gathered} (x,\text{ y) }\rightarrow\text{ (-y, x)} \\ A\text{ becomes: (-(-3), 1) = (3, 1)} \\ B\text{ becomes: (-0, 3) = (0, 3)} \\ C\text{ becomes: (-(-2), }4\text{) = (2, 4)} \end{gathered}[/tex]Next we will apply reflection over the x axis:
negate y coordinate while keeping x coordinate constant
[tex]\begin{gathered} (x,\text{ y) }\rightarrow(x,\text{ -y)} \\ (3,\text{ 1) becomes (3 -1)} \\ A^{\prime}\text{ = (3, -1)} \\ \\ (0,\text{ 3) becomes (0, -3)} \\ B^{\prime}\text{ = (0, -3)} \\ \\ (2,\text{ 4) becomes (2, -4)} \\ C^{\prime}\text{ = (2, -4)} \end{gathered}[/tex]I answered a few of these already. Am I right? What are the others? Thank you.
Answers
Answer:
Step-by-step explanation:
1. Number 1 is correct.
2. Number 2 is base angles.
3. Number 3 is correct.
4. Number 4 is vertical angles.
5. Number 5 is alternate interior angles.
6. Number 6 is corresponding parts.
7. Number 7 is correct.
8. Number 8 is vertex angles.
9. Number 9 is reflexive property.
10. Number 10 is correct.
Good luck! I hope you give me brainliest!
Sarah spends of her monthly take-home pay on rent, food, and clothing. If she earns $1,830 in take-home pay each month, how much does she spend on rent, food, and clothing? A$610 B $915 C $990 D $1,220 E $2,745
Answers
We have that Sarah spends 2/3 of $1,830 in rent food and clothing
In order to find the money she spends, we just have to divide $1,830 in 3 and multiply the result by 2:
[tex]\begin{gathered} \frac{1830}{3}=610 \\ 610\cdot2=1220 \end{gathered}[/tex]Answer - D. $1,220Write an equation that best describes the pattern in the table. 12 | 14 | 17 | 19 | 22 6 | 8 | 11 11 | 13 | 16 y у
Answers
We need two ordered pairs of the table
(12,6)=(x1,y1)
(14,8)=(x2,y2)
[tex]m=\frac{y_2-y_1}{x_2-x_1}=\frac{8-6}{14-12}=\frac{2}{2}=1[/tex]the equation is
[tex]\begin{gathered} y-6=1(x-12) \\ y=x-12+6 \\ y=x-6 \end{gathered}[/tex]the equation is
y=x-6
I need help with this practice problem solving It is trigonometry At the bottom of the picture is the answer options, one answer per box.
Answers
First, remember how does the graph of the function f(x) = tan(x) look:
For the inverse of a function to exist, the function has to be an injective function.
A function is injective if it passes the horizontal line test.
Since the function f(x) = tan(x) is periodic and its period is equal to π, its domain must be restricted to an interval of length π in order to pass the horizontal line test.
If we keep the piece of the graph that passes through the origin, we must restrict the domain of the tangent function to the interval (-π/2,π/2) for the function to be injective, and thus for the inverse of the function to be defined.
Therefore, in both cases the answer is:
[tex](-\frac{\pi}{2},\frac{\pi}{2})[/tex]d. 12/1312. Use the unit circle to find cos ( 7 )a.S S/-b.o. 1/2d. -1/2
Answers
Step 1
Write the trigonometric expression
[tex]cos(\frac{7\pi}{6})[/tex]Step 2:
Step 3
[tex]cos(\frac{7\pi}{6})\text{ = -cos\lparen}\frac{\pi}{6}\text{\rparen= -cos30}\degree\text{ = -}\frac{\sqrt{3}}{2}[/tex]Final answer
[tex]-\frac{\sqrt{3}}{2}[/tex]-11b+7=40 how do we solve for b?
Answers
We want to find the unknown value b in the following equation
-11b + 7 = 40
Since both sides are the same we can substract 7 both sides and it will be true
-11b + 7 - 7 = 40 - 7
-11b + 0 = 33
-11b = 33
We want to have just b in one side of the equation, we can divide both sides by -11, since they are equal:
-11b = 33
[tex]\begin{gathered} \frac{-11b}{-11}=\frac{33}{-11} \\ 1\cdot b=-3 \\ b=-3 \end{gathered}[/tex]Answer: b = -3Simplify: 8z + 5y + 6z + Зу * O 14z + 8y 13y + 9z O 22y 22z
Answers
Answer:
14z + 8y
Explanation:
Given the equation 8z + 5y + 6z + Зу
first is to collect the like terms;
8z + 5y + 6z + Зу
= (8z + 6z) + (5y + 3y)
= 14z + 8y
Hence the simplified form is 14z + 8y
Point O is the center of a regular hexagon. Find the image of C given the counter clock-wiserotation of r (120,0)ABFC сEDОЕOFОАOD
Answers
ANSWER:
A.
STEP-BY-STEP EXPLANATION:
Because a full turn is a total of 360°, since there are 6 sides, each side represents 60° (360°/6).
They tell us that point C. is rotated counterclockwise 120°.
Therefore, it would be to rotate two sides in that sense counterclockwise, since 120°/60° = 2
If we look closely, the artist who meets these characteristics is A.
Question 2 of 15, Step 1CorrectThe value of a machine, V, at the end of years is given by V = C(1 - 1), where is the original cost of the machine and r is the rate of depreciation. A machine thatoriginally cost $19,600 is now valued at $15,528. How old is the machine if r = 0.12? Round your answer to two decimal places.
Answers
If C = $19600, V = $ 15528 and r = 0.12, we have:
[tex]\begin{gathered} 15528=19600(1-0.12)^t \\ 15528=19600\cdot0.88^t \\ \frac{15528}{19600}=0.88^t \\ \frac{1941}{2450}=0.88^t \\ log(\frac{1,941}{2,450})=log(0.88^t) \\ log(\frac{1,941}{2,450})=t\cdot log(0.88^) \\ t=\frac{log(\frac{1,941}{2,450})}{log(0.88^)} \\ t=\frac{-0.101}{-0.056} \\ t\approx1.82\text{ years} \end{gathered}[/tex]Lines AB and CD at E. If m∠AEC=x^2+3x and m∠BED=6x+4 ,find m∠CEB.
Answers
Explanation
Step 1
when two lines intersect, vertical angles that are equal are formed.Also two angles are Supplementary when they add up to 180 degrees
then
[tex]\begin{gathered} m\measuredangle\text{AEC =}m\measuredangle BED \\ \text{replacing} \\ x^2+3x=6x+4 \end{gathered}[/tex]and
[tex]m\measuredangle\text{AEC}+\text{ m}\measuredangle CEB=180[/tex]Step 2
solve for x,
[tex]\begin{gathered} x^2+3x=6x+4 \\ x^2+3x-6x=+4 \\ x^2+3x-6x-4=0 \\ x^2-3x-4=0 \\ \text{factorize} \\ (x-4)(x+1)=0 \\ it\text{ means} \\ x-4=0 \\ x=4 \\ or \\ x+1=0 \\ x=-1 \end{gathered}[/tex]we just take the positive number, because we are searching for an angle ( angles and distance are always positives)
then
[tex]x=4[/tex]Step 3
replace the value of x in the angle AEC
[tex]\begin{gathered} m\measuredangle AEC=x^2+3x \\ m\measuredangle AEC=4^2+3\cdot4 \\ m\measuredangle AEC=16+12 \\ m\measuredangle AEC=28 \\ \end{gathered}[/tex]replace the value of AEC in equation (2) to find CEB
[tex]\begin{gathered} m\measuredangle\text{AEC}+\text{ m}\measuredangle CEB=180 \\ 28+m\measuredangle CEB=180 \\ \text{subtract 28 in both sides} \\ 28+m\measuredangle CEB-28=180-28 \\ m\measuredangle CEB=152 \end{gathered}[/tex]I hope this helps you.
of what theorem is theorem 21 the converse?theorem21:if the opposite sides of a quadrilateral are equal then the figure is a parallelogram
Answers
Theorem 1:
Opposite Sides Theorem Converse: If both pairs of opposite sides of a quadrilateral are congruent, then the figure is a parallelogram.
The shorter sides of a rectangle measure 4 inches eachand one of its diagonals measures 8 inches. Which ofthe following is the measure of one of its longer sides?
Answers
Lets draw a picture of the rectangle:
From our figure, we can note that triangle ABC is a right triangle, so we can apply Pythagorean theorem, that is
[tex]4^2+x^2=8^2[/tex]which gives
[tex]16+x^2=64[/tex]If we move 16 to the right hand side, we get
[tex]\begin{gathered} x^2=64-16 \\ x^2=48 \end{gathered}[/tex]Then, x is given by
[tex]x=\sqrt[]{48}[/tex]since 48 = 16 x 3, we get
[tex]\begin{gathered} x=\sqrt[]{16\times3} \\ x=\sqrt[]{16}\times\sqrt[]{3} \\ x=4\sqrt[]{3} \end{gathered}[/tex]therefore, the answer is
[tex]x=4\sqrt[]{3}[/tex]which is the measure of the longer side.
What is the missing length? y 16 km area = 144 km y = kilometers
Answers
Area = length x width
Area = 144km^2
length = 16km
width = y
144 = 16 x y
y = 144/6 = 26 km
y = 24km
Solve the y system of inequalities by choosing the correct graph.y> 3y< |x-2|
Answers
The solution graph of the system of inequalities : y> 3 and y< |x-2| is attached below.
The given inequalities are:
y>3 and y< |x-2|
Now we will solve y< |x-2|
applying absolute value we get
x - 2 < -y or x - 2 > y
Now we will solve the two equations graphically.
Using the graph we can clearly see that the red part represents the inequality y< | x - 2 | while the blue part denotes the inequality y > 3
Hence the solution of the two inequalities will be the region shaded by both the graphs.
Any monotonically increasing function can, by definition , be applied both for sides of just an inequality without distorting their relationship as long as both expressions fall inside the scope of the function. If a monotonically falling function are applied to both sides of an inequality, the inequality relation might be reversed.
To learn more about inequality visit:
https://brainly.com/question/20383699
#SPJ9
Which sequence of transformations maps polygon ABCD onto polygon WXYZ?
Answers
We have to find the transformations that led from polygon ABCD to WXYZ.
As the shapes are not equally oriented, we have to find if one of the transformation is a rotation or a reflection.
We can fin this by looking at the position of corresponding sides. So first, we have to find corresponding sides of the two polygons. The polygon WXYZ has also a scale transformation, so its size is proportional, with a proportion greater than 1 as it is bigger, to the size of ABCD.
Each side in the pre-image has a corresponding side in the image. Each corresponding side in the image will be k times bigger than the side in the pre-image, and this k is the same for the four sides.
We can look at the sides that are parallel to the axis, BC and CD, and see that CD is longer than BC. If we look at WXYZ, YZ is longer than YX.
Then, we can conclude that YZ and CD are corresponding sides as BC and YX.
The scale factor is k = 2 as YZ is twice as long as CD.
Then we can see, by the position of BC and CD respect to YX and YZ that no rotation can convert the pre-image into the image, so the orientation of the image is due to a reflection with axis of symmetry at x = 7.
Then, after the reflection, the image is dilated with a factor k = 2.
Answer:
B. A reflection of polygon ABCD followed by a dilation of the image with a scale factor of 2.
Answer:
B
Step-by-step explanation:
plato
I need this answered from my prep guide, I will include the picture of the answer options
Answers
SOLUTION
(a) The vertex of the parabola
[tex]\begin{gathered} (y+1)^2=12(x-3) \\ so,\text{ } \\ 12(x-3)=(y+1)^2 \end{gathered}[/tex]Now,
[tex]\begin{gathered} 4p\mleft(x-h\mright)=\mleft(y-k\mright)^2 \\ \mathrm{\: is\: the\: standard\: equation\: for\: a\: right-left\: facing\: parabola\: with\: vertex\: at}\: \: \\ \mleft(h,\: k\mright),\: \\ \mathrm{and\: a\: focal\: length\: }\: |p| \end{gathered}[/tex]From the initial equation we have
[tex]\begin{gathered} 12(x-3)=(y+1)^2 \\ 4\times3(x-3)=(y-(-1)^2) \\ \text{comparing to }4p(x-h)=(y-k)^2 \\ \text{vertex (h, k) = (-3, -1)} \end{gathered}[/tex]Therefore, the vertex of the parabola is (-3, -1)
(b) The parabola opens at?
Let us see the graph of the parabola
From the image, we can see that the Parabola opens right
(c) The focus
This can be determined using the formula
[tex]\begin{gathered} (h+p,-1) \\ \text{note from above that h = 3 and p = 3} \\ \text{the focus becomes } \\ (3+3,-1) \\ (6,-1) \end{gathered}[/tex]Now, the focus has coordinates (6, -1). Looking at the graph, we can see that from the point x = 6, the focus is 3 units away from the vertex.
(d) The directrix is read from point x = 0.
So, reading from x = 0, from the graph we can see that directrix is 6 units away from thr focus
From our explanation above, we can see that
(e) The focus is the point (6, -1)
(f) And the directrix is
[tex]x=0[/tex]Rewrite the following expression in exponential form. log, 0.04 = -2 O A. - 25 = 0.04 O B. 5-2=0.04 O c. 50.04 = -2 O D. 0.04 -² = 5 5 SUE PREVIOUS
Answers
Answer:
B
Select ALL the correct answers.Consider the geometric sequence below.Select all functions that define the given sequence-4, -6, -9, -27/2, -81/2
Answers
Given:
The geometric series
-4, -6, -9, -27/2, -81/2
Required:
Choose the correct option.
Explanation:
The given series is:
-4, -6, -9, -27/2, -81/2
The nth term of the geometric series is given by the formula:
[tex]a_n=ar^{n-1}[/tex]Where a = first term and r = common ratio
From the given series
a = -4
[tex]\begin{gathered} r=\frac{-6}{-4} \\ r=\frac{3}{2} \end{gathered}[/tex]Thus the nth term is:
[tex]f(n)=-4(\frac{3}{2})^{n-1}\text{ where n =2,3,4,.....}[/tex]Final Answer:
[tex][/tex]Write the equation in slope-intercept form and then graph the equation that passes through (5, -7) and is parallel to to y = −4x + 3
Answers
The slope-intercept form is:
[tex]y=mx+b[/tex]Where m is the slope and b is the intercept.
For two lines to be parallel they have to have the same slope. So a line parallel to
[tex]y=-4x+3[/tex]Has m = -4. So until now we have this equation:
[tex]y=-4x+b[/tex]To find the intercept b we use the given point (5,-7). We just have to replace these values of x and y into the equation above and solve for b:
[tex]\begin{gathered} -7=-4\cdot5+b \\ -7+20=b \\ 13=b \end{gathered}[/tex]So there we have the complete equation of the asked line:
[tex]y=-4x+13[/tex]And the graph is:
Use the graph to answer the questionWhat is the average rate of change of f(x) between P and Q?
Answers
The average rate of change of a function over a interval [a,b] is given by:
[tex]r=\frac{f(b)-f(a)}{b-a}[/tex]Where, in this case:
[tex]\begin{gathered} a=1 \\ b=2 \\ f(a)=0 \\ f(b)=3 \\ so: \\ r=\frac{3-0}{2-1}=\frac{3}{1}=3 \end{gathered}[/tex]Answer:
D. 3
Instructions: Given the coordinate points of the preimage, use the transformation given to provide the points of the image. V(-5,-2) W(-2,1) X(-3,-3) Rotation: 90º about the origin v' W'( X'(3 -3 > Check
Answers
The rotation is 90 degree about the origin. The rule can be express below
[tex](x,y)\rightarrow(y,-x)[/tex]Therefore,
[tex]\begin{gathered} V(-5,-2)\rightarrow V^{\prime}^{}(-2,5) \\ W(-2,1)\rightarrow W^{\prime}(1,2) \\ X(-3,-3)\rightarrow X^{\prime}(-3,3) \end{gathered}[/tex]Note this is a clockwise 90 degree rotation.
What is the area of the figure? Round to the nearest tenth if necessary. Include units in your answer.
Answers
We can think of a hexagon in the next way:
This is, a shape made of 6 smaller triangles. So, we only need to calculate the area of one of those triangles and multiply it by 6
There is something interesting, each of the angles of every one of the triangles is 60°, those are equilateral triangles. So, let's focus on one triangle:
Notice that the blue line is the height of the triangle, that's what we need to find it's are using the formula:
[tex]A(triangle)=\frac{hb}{2}[/tex]So, to calculate the height we use the Pythagoras Theorem
[tex]H^2-O^2=b^2\Rightarrow(20\operatorname{cm})^2-10\operatorname{cm}=b^2\Rightarrow b^2=300\operatorname{cm}\Rightarrow b=10\sqrt[]{3}[/tex]Finally, the area of one of the triangles is:
[tex]A(triangle)=\frac{1}{2}(20cm)(10\sqrt[]{3}cm)=173.2cm^2[/tex]And, by multiplying the previous result by 6, we get the area
[tex]A(hexagon)=6\cdot A(triangle)=6(173.2cm^2)=1039.2\operatorname{cm}[/tex]What is the least common multiple of 3,4,and 8
Answers
Answer:the least common multiple of 3, 4, 8 is 48
Step-by-step explanation:
Answer:
24
Step-by-step explanation:
valuate the expression when x = 10. Show your work, and explain each step you take 5x = 152.Evaluate the expression when b = 5 and h = 6. Show your work and explain each step you take 1/2b*h
Answers
In the first part, we have the followed expression:
[tex]5x\text{ - 15}[/tex]Wants to know the value of it when x=10, so we just need to substitute the value in the expression, wich gives us:
[tex]5\times(10)\text{ - 15, wich give us the expression: 50 - 15 = 35}[/tex]In the second part, we have the expression:
[tex]\frac{1}{2}b\times h[/tex]And we want to know the value of it when b=5 and h=6, so lets substitute those values in our expression:
[tex]\frac{1}{2}(5)\times(6),\text{ wich gives us, }\frac{1}{2}30\text{ = }\frac{30}{2}\text{ = 15}[/tex]A rectangular window is 48 in long and 24 in wide.Christine would like to buy a screen for the window. Thecost of the screen is based on the number of squarefeet the screen is. Use the facts to find the area of thewindow In square feet.Conversion facts for length1 foot (ft) = 12 inches (in)1 yard (yd) = 3 feet (ft)1 yard (yd) = 36 Inches (in)x 6 ?
Answers
we have that
1 ft=12 in
so
L=48 in
Convert to ft
48 in=48/12=4 ft
W=24 in
24 in=24/12=2 ft
therefore
the area is (4*2=8 ft2)
What is the term-to-term rule for the following sequences? Solve (A)A) 1,2,3,4,5,6,7,8,…B) 4,9,14,19,24,29,…C) 32,30,28,26,24,22,…D) 6,13,20,27,34,41,…E) 3,6,12,24,48,96,…F) 36,30,24,18,12,6,…G) -13,-11,-9,-7,-5,…H) 48,45,42,39,36,…I) 1,7,49,343,2401,…
Answers
A) Given:
The sequence is,
[tex]1,2,3,4,5,6,7,8,…[/tex]To find: The term-to-term rule
Since the given sequence has the common differnce 1.
So, it is of the arithmetic sequence.
Therefore, let us take
[tex]a_1=1[/tex]Then the second term will be,
[tex]\begin{gathered} a_2=a_1+1 \\ =1+1 \\ =2 \end{gathered}[/tex]The third term will be,
[tex]\begin{gathered} a_3=a_2+1 \\ =2+1 \\ =3 \end{gathered}[/tex]And so on.
So, the term to term rule must be,
[tex]a_n=a_{n-1}+1[/tex]Final answer: The term to term rule is,
[tex]a_{n}=a_{n-1}+1[/tex]I have this practice question from my ACT prep guide, THE SUBJECT IS PRE CALC!! MEANING ITS HARD AND COMPLEX. Below will be the questions to this problem ( includes 5 questions )1. What is the balance of Albert’s $2000 after 10 years? 2. What is the balance of Marie’s $2000 after 10 years? 3. What is the balance of Han’s $2000 after 10 years?4. What is the balance of Max’s $2000 after 10 years? And lastly, 5. Who is $10,000 richer at the end of the competition?
Answers
Albert
Compound interest formula:
[tex]A=P(1+\frac{r}{n})^{nt}[/tex]where:
A: final amount
P: principal
r: annual interest rate, as a decimal
t: time in years
n: number of times interest applied per year
Substituting with P = $1000, r = 0.012 (= 1.2/100), n = 12 (interest is compounded monthly), t = 10 years, we get:
[tex]\begin{gathered} A=1000(1+\frac{0.012}{12})^{12\cdot10} \\ A=1000(1.001)^{120} \\ A=1127.43\text{ \$} \end{gathered}[/tex]If $500 lost 2%, then it keeps 98% of its original value, that is,
$500x98% = $490
Continuous compound formula:
[tex]A=Pe^{rt}[/tex]where the variables have the same meaning as before.
Substituting with P = $500, r = 0.008 ( = 0.8/100), and t = 10 years, we get:
[tex]\begin{gathered} A=500\cdot e^{0.008\cdot10} \\ A=541.64\text{ \$} \end{gathered}[/tex]The balance of Albert’s $2000 after 10 years is:
$1127.43 + $490 + $541.64 = $2159.07
Marie
Substituting in the compound interest formula with P = $1500, r = 0.014 (= 1.4/100), n = 4 (interest is compounded quartely), t = 10 years, we get: