When solving the system below algebraically using the substitution method, which of the following could be an equation you could create to solve for y?A. -4(2y - 20) + 3y = 30B. -4(-2y + 20) + 3y = 30C. -2y + 20 = -3y + 30D. 4(x + 2y = 20
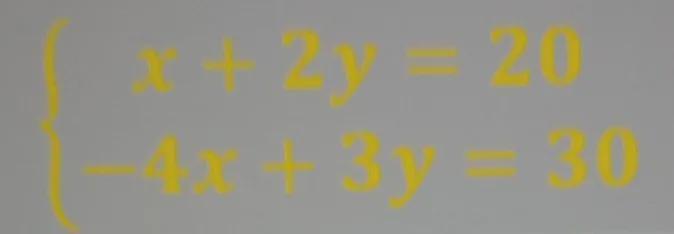
Answers
The goal of the substitution method is to eliminate one of the variables using one of the equations of the systems. We are told that we want to solve for y, that is, we should use one equation to eliminate the variable x.
Since the coefficient of x in the first equation is 1, we will use the first equation to eliminate x in the second equation. So, we have the first equation
[tex]x+2y=20[/tex]So, by subtracting 2y on both sides, we get
[tex]x=20-2y[/tex]which is equivalent to
[tex]x=-2y+20[/tex]So, if we replace this value of x in the second equation,w e get
[tex]-4\cdot(-2y+20)+3y=30[/tex]which corresponds to option B
Related Questions
What is the real part of 4 – 5i? 54-5i-5
Answers
Every imaginary number have the following form:
[tex]a\text{ +bi (1)}[/tex]Where a= real part , b= imaginary part
Basically on this case the real part would be the number without the i and the imaginary part the number with i
The real part is:
[tex]4[/tex]And the imaginary part:
[tex]-5[/tex]Final answer:
[tex]4[/tex]The number of needles in each packet are 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 5, 6, 7,and 8. Find the range of the given data.
Answers
Given that
The number of needles in the packet is 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, 5, 6, 7, 8
And we have to find the range of this data.
Explanation -
To find the range first we will arrange the numbers in the order as
1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 6, 7, 8
Now we will subtract the lowest number from the highest to get the range.
So
nge = 8 - 1 = 7
Final answer -
Hence the range is 7, So the final answer is 7.Consider the diagram and angle measures shown below.m∠1 = (3x +25)m∠2 = (7x+5)m∠3 =(-2x + 70)4322 || 7What is the value of m∠3 ?
Answers
First, we need to find the value of x
m<4 = m<1 = (3x + 25)° ( corresponding angle)
Let the angle between m<2 and m<3 be m<5
m< 5 = m<4 = (3x + 25)° ( vertical angle)
m<2 + m<5 + m<3 = 180° (angles on a straight line
(7x+5)° + (3x+25)° + (-2x + 70)° = 180°
7x + 5 + 3x + 25 -2x + 70 = 180
Rearrange
7x + 3x -2x + 5 + 25 + 70 = 180
8x + 100 = 180
subtract 100 from both-side of the equation
8x = 180 - 100
8x = 80
Divide both-side of the equation by 8
x = 10
m<3 = -2x + 70
substitute x = 10 in the above
m<3 = -2(10) + 70 = -20 + 70 = 50°
Find mZ1 in the picture below.1(3y² + 2y – 10)(2y² + 7y + 4)
Answers
m∠1=29
In this question,
1) Since we have, vertical angles, whose measure are written as polynomials then we can write according to the Vertical angles theorem:
3y² + 2y – 10 =2y² + 7y + 4
3y²-2y² -7y+2y-10-4=0
y²-5y-14=0
1.1) Finding the roots by Sum and Product
S(x) = ___ +___ = -5
P(x) =____ x ___ = -14
x1=-2 or 7
Since our Domain, cannot allow negative numbers, let's keep the positive one 7
2) Moreover to that, m∠1 + 2y² + 7y + 4 = 180º
m∠1 +2(7)²+7(7)+4=180
m∠1 +151 =180
m∠1=180-151
m∠1=29
Choose ALL answers that describe thequadrilateral DEFGit DE FG,EF | GD, diagonal DF = 16, and diagonalEG=16.
Answers
Having two sets of parallel lines means that it can either be a rectangle, a square, a parallelogram, or a rhombus.
Having the diagonals congruent makes this figure either a rectangle or a square.
Since the length of the side is not given, we can only assume that this is a rectangle.
Summarizing it all, quadrilateral DEFG is a parallogram that is a rectangle because of the two pairs of parallel lines, and it has congruent diagonals.
The composition of rigid motions T(10,- 27 OT(-24,4, describes the route of a limousine in a city from its starting position. Describe the route in words. Assume that the positive y-axis points north. block(s) north, and then it drives 3 block(s) west and 4 block(s) north. First the limousine drives 2 block(s) east and (Type whole numbers.)
Answers
The problem describes two operations of translation on the car. The first operation says that the car translated "10" units on the x-coordinate and "-2" units on the y-coordinate.
When translations are performed on the "x-coordinate" if they are positive, the function is moved to the left and if they are negative the function is moved to the right. When translations are performed on the "y-coordinate" if they are positive the function is moved up and if negative, the function is moved down.
Since the first translation on the x-axis was positive, then the car moved to the left 10 units, which would be "10 blocks" on the west direction. The translation on the y-coordinate was negative, so the function moved down. The car moved "2 blocks" on the south direction.
The second translation is (-24, 4). The translation on the x-axis is negative so the car is moved 24 units to the east direction. The translation on the y-axis is positve so the car is moved 4 units on the north direction.
The final answer is:
First the limousine drives 10 blocks west and 2 blocks south and then it drives 24 blocks east and 4 blocks north.
Countries represented at each festival 6 5 4 Number of festivals 3 N 1 0 0-5 6-11 12-17 18-23 24-29 Number of countries How many festivals had 12 or more countries represented.
Answers
11 festivals
Explanation
to find the nunmber of festivals that had 12 or more countries, sum the festivals for all values in number of countries greather than 12, it its
[tex]\begin{gathered} \text{column 3 (12-17)=5 festivals} \\ \text{column 4(18-23)=4 festivals} \\ column5(24-29)=2\text{ festivals} \\ so,\text{ the total of festivals for 12 or more countries is} \\ \text{total}=5+4+2 \\ total=11\text{ festivals} \end{gathered}[/tex]I hope this helps you
Sam is building a model of an antique car. The scale of his model to the actual1car is 1:10. His model is 15 1/2 inches long. How long is the actual car?215The length of the actual car isinches.
Answers
The car is 10 times the size of the model.
So, we have to multiply the length of the model by 10.
15 1/2 x 10 =
(15x2+1)/2 x 10=
31/2 x10 =310/2 = 155
The length of the actual car is 155 inches
What are the leading coefficient and degree of the polynomial?-8u^6-15+4u+18u^9
Answers
The degree of a polynomial is given by the higher exponent of the variable.
In this polynomial, we have terms with the variable with exponents 6, 0, 1 and 9.
Therefore the degree of the polynomial is 9.
The leading coefficient is the number that multiplies the variable with a higher exponent.
The leading term is 18u^9, so the leading coefficient is 18.
1990, the cost of tuition at a large Midwestern university was $101 per credit hour. In 2005, tuition had risen to $236 per credit hour.
Answers
Solution:
According to the problem, the linear equation would be:
[tex]C(X)=101+9(x-1990)[/tex]now, if x=2013, the tuition will be:
[tex]C(2013)=101+9(2013-1990)=101+9(23)[/tex]this is equivalent to
[tex]C(2013)=101+9(23)=308[/tex]7. Translate the following Marco has $6 less than Ann has
Answers
Solution:
Let x represent the amount Marco has,
let y represent the amount Ann has.
Given that Marcos has $6 less than Ann has, this implies that
[tex]\begin{gathered} x=y-6 \\ \end{gathered}[/tex]Ann has
[tex]y[/tex]Marco has
[tex]y-6[/tex]Kelly is building a playpen for her dog. The area of the playpen is 22.75 square feet. The length is 6.5 feet and the width is w feet.
Answers
w = 3.5 feet
Explanation:Area = 22.75 square feet
length = 6.5 feet
width = w
Since we have beeen given dimensions in the form of length and width, the shape at the play house is a rectangle:
Area of rectangle = length × width
22.75 square feet = 6.5 feet × w
22.75 = 6.5w
divide both sides by 6.5:
22.75/6.5 = 6.5w/6.5
w = 3.5 feet
At the city museum, child admission is $5.90 and adult admission is $9.40. On Saturday, 170 tickets were sold for a total sales of $1332.00. How many adulttickets were sold that day?Number of adult tickets:
Answers
In this case, we'll have to carry out several steps to find the solution.
Step 01:
data:
city museum
Step 02:
system of equations:
x = # child tickets
y = # adult tickets
equations:
x + y = 170 eq. 1
5.90x + 9.40y = 1332 eq.2
x + y = 170 * (- 5.90)
5.90x + 9.40y = 1332
-5.90x - 5.90y = - 1003
5.90x + 9.40y = 1332
--------------------------------
3.5y = 329
y = 329 / 3.5
y = 94
The answer is:
# adult tickets = 94
The figure shows a person estimating the height of a tree by looking at thetop of the tree with a mirror. Assuming that both the person and the tree formright angles with the ground, which of the following proportions can be usedto estimate the height of the tree?6 ft3 ft7 fthft
Answers
SOLUTIONS
Using the rule of SOHCAHTOA:
The height of the tree compared to the height of the boy is tangent:
[tex]tan\theta=\frac{opp}{adj}[/tex]For the small triangle:
[tex]tan\theta=\frac{6}{3}.........(1)[/tex]For the Big triangle:
[tex]tan\theta=\frac{h}{7}..........(11)[/tex]Equating (1) and (11
[tex]\begin{gathered} \frac{6}{3}=\frac{h}{7} \\ \frac{6}{h}=\frac{3}{7} \end{gathered}[/tex]Hence the correct answer = Option A
What is the congruence correspondence, if any, that will prove the given triangles congruent?A. SASB. AASC. noneD. ASA
Answers
None (option C)
Explanation:Congruent triangles have same shape and size
Rules that can be used to prove triangle congruency:
SAS - side angel side
AAS = Angle angle Side
SSS = side-side-side
ASA = Angle-side-angle
From the triangles given, we see they are not of the same size even though they look alike.
Also the corresponding angles of both triangles do not look the same.
As a result, we do not have conguruence correspondence that will prove the triangles are congruent.
None
In the expansion of (2a+4b)^8, which of the following are possible variable terms? Explain your reasoning?
Answers
In the expansion of (2a+4b)⁸ the possible variable terms are a⁸, a⁵b³, a³b⁵, a⁷b, and b⁸.
What is an Expression?
In mathematics, an expression is defined as a set of numbers, variables, and mathematical operations formed according to rules dependent on the context.
We need to find the possible variable terms in the expansion of (2a+4b)^8
The given expression can be written as:
(2a + 4b)⁸ = (2a + 4b)² x (2a + 4b)² x (2a + 4b)² x (2a + 4b)²
= (4a² + 8ab + 16b²) x (4a² + 8ab + 16b²) x (4a² + 8ab + 16b²) x (4a² + 8ab + 16b²)
Now, further simplify the above expression.
(16a⁴ + 32a³b + 64a²b² + 32a³b + 64 a²b² + 128b⁴ + 64a²b² + 128ab³ + 256b⁴) x (16a⁴ + 32a³b + 64a²b² + 32a³b + 64 a²b² + 128b⁴ + 64a²b² + 128ab³ + 256b⁴)
Hence, In the expansion of (2a+4b)⁸ the possible variable terms are a⁸, a⁵b³, a³b⁵, a⁷b, and b⁸.
To learn more about Expression refer here
brainly.com/question/13947055
#SPJ9
Part 311Use the relationships in circle O to find the missing measures in circle S.1 pointIf WR = 12 units and MN = 8 units, determine MW.Type your answerwMRNePrestipus
Answers
From the properties of secant line and the tangent to the circle
If a secant segment and tangent segment are drawn to a circle from the same external point, the length of the tangent segment is the geometric mean between the length of the secant segment and the length of the external part of the secant segment.
[tex]\frac{Whole\text{ Secant}}{\tan gent\text{ Line}}=\frac{\tan gent}{External\text{ Secant Part}}[/tex]
In the given figure we hvae :
Whole secant length (RM),
Tangnt line MN = 8 units
External secant part (WM)
Since RM = WR + WM
RM=12 + WM
Susbtitute the value:
[tex]\begin{gathered} \frac{Whole\text{ Secant}}{\tan gent\text{ Line}}=\frac{\tan gent}{External\text{ Secant Part}} \\ \frac{RM}{MN}=\frac{MN}{MW} \\ \frac{12+MW}{8}=\frac{8}{MW} \\ \text{Apply crossmultiplication:} \\ MW(12+MW)=8\times8 \\ 12MW+(MW)^2=64 \\ \text{ Let MW = x} \\ 12x+x^2=64 \\ x^2+12x-64=0 \\ \text{ Factorize:} \\ x^2+16x-4x-64=0 \\ x(x+16)-4(x+16)=0 \\ (x-4)(x+16)=0 \\ \text{ So, x = 4, -16} \\ \text{ Since measurement cannot be negative thus: x = 4 unit} \\ x\text{ = }MW=4 \end{gathered}[/tex]Answer : MW= 4 units
A painting sold for $216 in 1977 and was sold again in 1985 for $467. Assume that the growth in the value V of the collectors items was exponential.
A. Find the value k of the exponential growth rate. Assume v=216
K=?
Answers
The value k of the exponential growth rate is k = 0.1012
For given situation, we use the formula for exponential growth :
V(t) = V0(1 + k)^t
where, V(t) is the value of the collectors items
V0 is the initial value of painting
k is the exponential growth rate
t is the time interval
A painting sold for $216 in 1977 and was sold again in 1985 for $467.
So, V0 = $216
t = 1985 - 1977
t = 8
V(8) = $467
We need to find k
V(8) = V0(1 + k)^8
467 = 216 * (1 + k)^8
2.162 = (1 + k)^8
taking 8th root on both the sides,
1 + k = ± (2.162)^(1/8)
1 + k = (2.162)^(1/8) or 1 + k = -(2.162)^(1/8)
k = 0.1012 or k = -2.1012
Therefore, the value k of the exponential growth rate is k = 0.1012
Learn more about the exponential growth here:
https://brainly.com/question/11743945
#SPJ1
which system of equations is better to start up to solve using the subsition method or the elemination method?
Answers
For the set of equations, the answer will be:
The elimination method is better because both equations are in general form.
what is the lcm of 25 and 37?
Answers
SOLUTION:
Step 1:
In this question, we are meant to find the LCM of 25 and 37.
Step 2:
The least common multiple, lowest common multiple, or smallest common multiple of two integers a and b, usually denoted by lcm(a, b), is the smallest positive integer that is divisible by both a and b
The following dataset represents the dollar amounts of donations collected at the entrance to a free museum during onehour:5, 10,5,5, 15, 1, 10, 10,5,600,5Is the mean a reasonably good measure of central tendency for this dataset? What if the outlier were removed fromconsideration?
Answers
Given the data set :
5, 10, 5, 5, 15, 1, 10, 10,5, 600, 5
As seen most of th data is between 1 and 15 except one data is 600
so, 600 represents an outlier for the data
so, the answer is option 4
Precalculus:Consider the right triangle where a = 3mi and alpha = 45 degrees Find an approximate value (accurate up to three or more decimals) of each of the following. Give the angle in degrees.
Answers
Given:
[tex]\begin{gathered} a=3mi \\ \alpha=45\degree \end{gathered}[/tex]Required:
To find the value of beta, b and c.
Explanation:
The given triangle is right triangle.
Therefore,
[tex]\begin{gathered} \sin\alpha=\frac{a}{c} \\ \\ \sin45=\frac{3}{c} \\ \\ 0.7071=\frac{3}{c} \\ \\ c=\frac{3}{0.7071} \\ \\ c=4.2426mi \end{gathered}[/tex]Now
[tex]\begin{gathered} \tan\alpha=\frac{a}{b} \\ \\ \tan45=\frac{3}{b} \\ \\ 1=\frac{3}{b} \\ \\ b=3 \end{gathered}[/tex]The sum of the angle in triangle is 180 degree.
Therefore
[tex]\begin{gathered} 90+45+\beta=180 \\ \beta=180-90-45 \\ \beta=45\degree \end{gathered}[/tex]Final Answer:
[tex]\begin{gathered} b=3mi \\ c=4.2426mi \\ \beta=45\degree \end{gathered}[/tex]find the correct area
Answers
we have that the area of the semicircle is 100,530964915 m^2
[tex]\begin{gathered} A\text{ = }\frac{\pi r^2}{2} \\ =\text{ }\frac{\pi(8m)^2}{2}=\text{ }32\pi m^2 \\ =\text{ }100,530964915m^2 \end{gathered}[/tex]Now we need to find the area of the triangle, we now that the area of the non rectangle triangle is 96 m^2
[tex]\begin{gathered} A\text{ = }\frac{b\cdot h}{2}\text{ = }\frac{16m\cdot\text{ 12m}}{2} \\ =\text{ }\frac{192m^2}{2}=96m^2 \end{gathered}[/tex]So the area of the figure is 196,530964915, the answer is 196.5 m^2.
I hope you are having a blessed day. Question is attached as a screenshot. Thank you :)
Answers
Solution:
Given the graphs of
[tex]\begin{gathered} y=x, \\ y=-x+4, \\ y=0 \end{gathered}[/tex]to be as plotted below:
The region ABC is bounded as shown above.
To find its area, the region ABC takes the shape of a triangle. Thus, we are to evaluate the area of the triangle ABC.
Step 1: Evaluate the midpoint between the distance AB.
The midpoint (x,y) of the distance AB is evaluated as
[tex]\begin{gathered} (x,y)=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) \\ \text{where} \\ x_1=0,y_1=0,x_2=2,y_2=2 \\ \text{thus,} \\ (x,y)=(\frac{0+2}{2},\frac{0+2}{2}) \\ =(1,1) \end{gathered}[/tex]Thus, the midpoint of the distance AB is (1,1).
Step 2: Evaluate the height of the region (triangle).
The height of the region is the same as the distance between points A and the midpoint of the distance AB.
Thus,
The distance is evaluated as
[tex]\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ x_1=2,y_1=2,x_2=1,y_2=1 \\ \text{thus,} \\ d=\sqrt[]{(1_{}-2_{})^2+(1_{}-2_{})^2} \\ =\sqrt[]{(-1_{})^2+(-1_{})^2} \\ =\sqrt[]{1+1} \\ d=\sqrt[]{2} \end{gathered}[/tex]Step 3: Evaluate the distance between points B and C.
The distance is evaluated similarly as
[tex]\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where} \\ x_1=0,y_1=0,x_2=4,y_2=0 \\ \text{thus,} \\ d=\sqrt[]{(4_{}-0_{})^2+(0_{}-0_{})^2} \\ =\sqrt[]{4^2+0^2} \\ d=4\text{ units} \end{gathered}[/tex]Step 4: Evaluate the area of the triangle ABC.
Given that the distance BC is 4 units and the height of the region is √2 units, the area of the region ABC is evaluated as the area of the triangle ABC.
Thus,
[tex]\begin{gathered} \text{Area = }\frac{1}{2}\times4\times\sqrt[]{2} \\ \Rightarrow Area\text{ =2}\sqrt[]{2} \end{gathered}[/tex]Hence, the area of the region is
[tex]2\sqrt[]{2}[/tex]The fourth option is the correct answer.
a crate is 24cm by 18cm by 15cm. it has to be packed with boxes that are 8cm by 6cm by 5cm. what is the largest number of boxes that can fit in the crate.
please help its level 2
show answer and working out.
Answers
The maximum no. of small boxes that can fit is 27 boxes.
What is a cuboid?A cuboid is a three-dimensional closed figure which has volume along with surface area.
The volume of a cuboid is the product of its length, width, and height.
The total surface area of a cuboid is 2( lw + wh + wl) and the lateral surface area is 2(l + w)×h.
Given, A crate is 24cm by 18cm by 15cm and it has to be packed with boxes that are 8cm by 6cm by 5cm.
Now, the maximum no of small boxes that can fit is the volume of the larger box divided by the volume of the sampler box which is,
= (24×18×15)/(8×6×5).
= 3×3×3.
= 27 boxes.
learn more about cuboid here :
https://brainly.com/question/19754639
#SPJ1
Jose is riding his bicycle. He rides for 14.4 kilometers at a speed of 9 kilometers per hour. For how many hours does he ride?hours:
Answers
Given:-
Jose rides 14.4 kilometers at a speed of 9 kilometers.
To find:-
The amount of hours he ride.
The formula used to find the time is,
[tex]time=\frac{Dis\tan ce}{speed}[/tex]Subsituting the value we get,
[tex]\begin{gathered} t=\frac{14.4}{9} \\ t=1.6 \end{gathered}[/tex]So the amount of hours jose rides is 1.6 hours.
i have no idea how to do this please help
Answers
Answer:
D. -1
Explanation:
• There are 5 x(s)
,• There are 6 1-boxes.
The equation modeled is:
[tex]5x+6=1[/tex]We solve for x.
[tex]\begin{gathered} 5x=1-6 \\ 5x=-5 \\ x=-\frac{5}{5} \\ x=-1 \end{gathered}[/tex]The value of x that makes the equation true is -1.
If the spinner is spun, what is the probability that the spinner will land on a multiple of 4?
Answers
Answer: A
Step-by-step explanation:
There are 10 possible outcomes on the spinner listed 1-10.
The multiples of 4 are 4, 8, 12, 16, and so on.
On the spinner, there are only 4 and 8 (of the multiples), and out of the 10 outcomes, that's 2/10 of them both.
If you multiply that fraction by 10 (we multiply by 10 since 2/10 isn't on the answer choices, also a number over 100 is also a percent)
that gives us 20/100, or 20%.
Hope that helps!
17 * 7*20000000000000
Answers
Here, we want to multiply the given terms
The best way to go about this
Answer: 2.38e+15
Step-by-step explanation:
How is a number related to its opposite?
Answers
The opposite of any given number is simply that number multiplied by negative 1. For instance, the opposite of 15 is 15 x (-1) and that is -15.
Therefore, a number is always a negative of its opposite