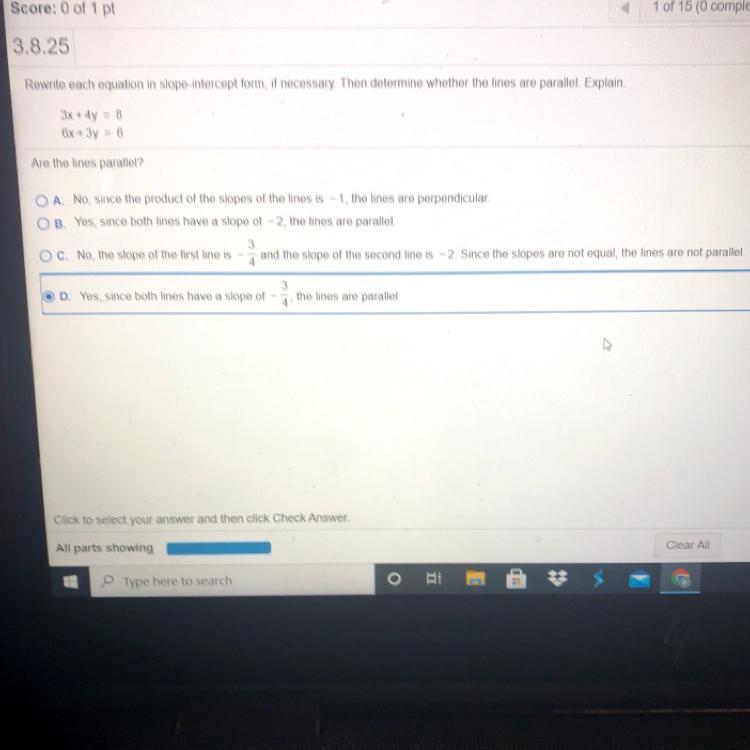
Rewrite each equation in slope intercept form, if necessary. Then determine whether the lines are parallel. Explain3x+4y = 86x+3y = 6Are these lines parallel?A.B.C.D.(look at image for answer choices)
Answers
We can rewrite the next equations in the slope-intercept form:
The first equation:
[tex]3x+4y=8\Rightarrow4y=8-3x\Rightarrow y=\frac{8}{4}-\frac{3}{4}x\Rightarrow y=2-\frac{3}{4}x\Rightarrow y=-\frac{3}{4}x+2[/tex]The second equation:
[tex]6x+3y=6\Rightarrow3y=6-6x\Rightarrow y=\frac{6}{3}-\frac{6}{3}x\Rightarrow y=2-2x\Rightarrow y=-2x+2_{}[/tex]As we can see, the slope of the first line is m = -3/4, and the slope of the second line is m = -2. Then, since the slope is different, these lines are not parallel (Option C).
Related Questions
Reason quantitatively. The two rectangles shown
are similar. What is the value of x
Answers
Two shapes are similar if the ratio of the lengths of their corresponding sides are equal.
Both shapes given in the question are rectangles, therefore, one pair of opposite sides is longer than the other.
We can find the ratio for the bigger rectangle since it has all the values complete and then compare this ratio to the smaller rectangle to find the value of the unknown side.
The ratio of the longer side to the shorter side for the bigger rectangle is
[tex]\begin{gathered} \frac{16}{2} \\ =8 \end{gathered}[/tex]Therefore, for the smaller rectangle, the ratio of the longer side to the shorter side is
[tex]\frac{4}{x}=8[/tex]Solving for x, we have
[tex]\begin{gathered} x=\frac{4}{8} \\ x=0.5 \end{gathered}[/tex]The value for x is 0.5.
Find the solution of the system of equations. 5x + 10y = -5 -5x - y = 32
Answers
5x + 10y = -5 ------------------------------(1)
-5x - y = 32 -------------------------------(2)
Add equation(1) and equation (2)
9y = 27
Divide both-side of the equation by 9
y = 3
Substitute y = 3 into equation (1) and solve for x
5x + 10(3) = -5
5x + 30 = -5
substract 30 from both-side of the equation
5x = -5 - 30
5x = -35
Divide both-side of the equation by 5
x = -7
The solution is (-7, 3)
Reflection over the y-axis Example 2 Original Point Coordinates Image Point Coordinates A (-8,2) A B (-4,9) B C (-3,2) C'
Answers
We have to reflect the 3 points shown over the y-axis.
The simple rule for reflecting over y-axis:
• keep y coordinate same
,• negate the x coordinate
So,
(x,y) would become (-x,y)
Now, let's reflect the 3 points:
A(-8,2) would become A'(8,2)
B(-4,9) would become B'(4,9)
C(-3,2) would become C'(3,2)
Hello did i do the graph right ? i needed to only plot my image
Answers
Given:-
[tex](10,10),(1,5),(10,7),(5,7),(1,8),(7,7)[/tex]To find:-
Plot the given points.
The graph of the given points is,
I need help with my math
Answers
Answer:
Jeff's popcorn container will hold more popcorn
The bigger container will hold 130 cubic cm more popcorn than the smaller container
Jeff's popcorn container has the following measurement
20.5cm x 10cm x 10cm
George's container has the following measurement
30cm by 8cm by 8cm
Volume of each container can be calculated as = Length x width x height
Volume of Jeff's container = 20.5 x 10 x 10 = 2, 050 cubic cm
Volume of George's container = 30 x 8 x 8
Volume of George's container = 1, 920 cubic cm
Therefore, Jeff's popcorn container will hold more popcorn
The bigger container = 2,050 cubic cm
The smaller container = 1, 920
The amount of popcorn the bigger container can hold more = 2050 - 1920
= 130 cubic cm
Therefore, the bigger container can hold 130 cubic cm more popcorn than the smaller container.
Evaluate. 10/16 divided by 5/16
Answers
2
Explanation
Let's remember the rule to divide two fractions
[tex]\begin{gathered} \frac{a}{b}\text{ divided by }\frac{c}{d} \\ \frac{\frac{a}{b}}{\frac{c}{d}}=\frac{ad}{bc} \end{gathered}[/tex]so,
calculate by applying the formula
[tex]\begin{gathered} \frac{10}{16}\text{ divided by }\frac{5}{16} \\ \frac{\frac{10}{16}}{\frac{5}{16}}=\frac{10\cdot16}{5\cdot16}=\frac{10}{5}=2 \end{gathered}[/tex]therefore, the result is 2
I hope this helps you 2
how do you identify sets of real numbers?
Answers
The set of number that best describe each situation is shown below:
[tex]\begin{gathered} \text{Whole numbers: These are natural counting positve numbers. e.g 1,2,3,4,5,etc} \\ \text{Integers: These are whole numbers that are positive, negative and zero. e.g 0,1,-1,2,-2,etc} \\ Rational\text{ numbers: These are numbers that can be expressed in the form of }\frac{a}{b},\text{ where b}\ne0,1.\text{ e.g 1/2, 3/5 etc} \\ \text{Irrational numbers: These are numbers that can be expressed in the form of }\sqrt[]{p}\text{ wh}ere\text{ p is prime. e.g }\sqrt[]{2,}\text{ }\sqrt[]{3}\text{ etc} \end{gathered}[/tex]Real numbers in general are majorly sub-divided into two(2) and they are Rational and Irrational numbers.
A university class has 29 students: 14 are psychology majors, 9 are history majors, and 6 are nursing majors. The professor is planning to select two of thestudents for a demonstration. The first student will be selected at random, and then the second student will be selected at random from the remaining students.What is the probability that the first student selected is a psychology majorand the second student is a history major?Do not round your intermediate computations. Round your final answer to three decimal places.
Answers
from the question given:
14 psychology majors
9 history major
6 nursing major
there are 29 total students
The probability that thr first student selected at random is a psychology major is 14/29
The probability that the second student selected at random from the remaining students is a history major is 9/28
The probability that the first student chosen is psychology major a a
Given f(x) f(x) = (- x2 + 7), what is the value of f(4)?
Answers
Given the below function;
[tex]f(x)=(-x^2+7)[/tex]What does y equal? -y=5y-6
Answers
Subtract 5y from both sides of the equation:
[tex]-y-5y=5y-5y-6[/tex][tex]-6y=-6[/tex]Divide both sides by -6
[tex]-\frac{6y}{-6}=-\frac{6}{-6}[/tex][tex]y=1[/tex]2) 58, 67, 44, 72, 51, 42, 60, 46, 69Minimum :Maximum :Q,Q2:Q,
Answers
Given the following data set:
58, 67, 44, 72, 51, 42, 60, 46, 69
First, we will arrange the data in order from the least to the greatest.
42, 44, 46, 51, 58, 60, 67, 69, 72
The minimum = 42
The maximum = 72
Q2 = the median of the data = the number that in the middle
As the set has 9 data, so, the median will be the data number 4
Q2 = 58
To find Q1 and Q3 , the data will be divided into two equal groups
(42, 44, 46, 51), 58, (60, 67, 69, 72)
Q1 = the median of the first group = (44+46)/2 = 45
Q3 = the median of the second group = (67+69)/2 = 68
So, the answer will be:
Minimum : 42
Maximum : 72
Q1 : 45
Q2 : 58
Q3 : 68
By what factors could each equation be multiplied in order to solve the system by linear combination? 2x-3y=8 and 5x+4y=-3A. First equation by 2: second equation by 5 B. First equation by 3; second equation by 4 C. First equation by 3: second equation by 8 D. First equation by 4: second equation by 3
Answers
we have these equations
[tex]\begin{gathered} 2x-3y=8 \\ 5x+4y=-3 \end{gathered}[/tex]In order to solve this system for the x variable, we can multiply the first equation by 4 and the second by 3
This correspond to answer D.
A right rectangular prism has length 3 3 ft, width 13 ft, and height 23 ft. 1 You use cubes with fractional edge length ft to find the volume. How many cubes are there for each 3 of the length, width, and height of the prism? Find the volume. How many cubes are there for each of the length, width, and height of the prism? cubes, the width has The length has cubes, and the height has cubes.
Answers
First, we need to convert the mixed numbers into fractions
[tex]3\frac{1}{3}=\frac{3\cdot3+1}{3}=\frac{10}{3}\text{ ft}[/tex][tex]1\frac{1}{3}=\frac{1\cdot3+1}{3}=\frac{4}{3}\text{ ft}[/tex][tex]2\frac{1}{3}=\frac{2\cdot3+1}{3}=\frac{7}{3}\text{ ft}[/tex]To find how many cubes fit on the length, we need to divide 10/3 by 1/3, as follows:
[tex]\frac{\frac{10}{3}}{\frac{1}{3}}=\frac{10}{3}\cdot3=10[/tex]To find how many cubes fit on the width, we need to divide 4/3 by 1/3, as follows:
[tex]\frac{\frac{4}{3}}{\frac{1}{3}}=\frac{4}{3}\cdot3=4[/tex]To find how many cubes fit on the height, we need to divide 7/3 by 1/3, as follows:
[tex]\frac{\frac{7}{3}}{\frac{1}{3}}=\frac{7}{3}\cdot3=7[/tex]Then, the length has 10 cubes, the width has 4 cubes, and the height has 7 cubes.
The volume of each cube is:
[tex]V=a^3=(\frac{1}{3})^3=\frac{1}{27}ft^3[/tex]The number of cubes that fit in the rectangular prism is: 10x4x7 = 280. Therefore, the volume of the prism is
[tex]280\cdot\frac{1}{27}=\frac{270+10}{27}=\frac{270}{27}+\frac{10}{27}=10\frac{10}{27}ft^3[/tex]Not understanding what they want and how they get to it
Answers
SOLUTION
The image below shows the solution
If you are selling your house with a local realtor who requires a 5 Pete cent commission fee what can you expect to pay the realtor of your house sells for 170,000
Answers
2. Find the values of x, y, and z. The diagram is not to scale.A. x = 85, y = 95, z = 74B. x = 74, y = 85, z = 95C. x = 74, y = 95, z = 85D. x = 85, y = 74, z = 95
Answers
Answer:
D. x = 85, y = 74, z = 95
Explanation
The sum of interior angles in the big trangle is 180degrees. Hence;
38 + 57 + x = 180
95 +x = 180
x = 180 - 95
x = 85degrees
The angle x and z are also supplementary since they bith lie on the same stright line. Hence;
85 +
Similarly, the sum of angle in the smaller triangle is 180degrees hence;
11 + z + y = 180
11 + 95 + y = 180
106 + y = 180
y = 180 - 106
y = 74degrees
Hence the value of x, y and z are 85, 74 and 95 degrees respectively
i got question A &B i just can’t get C
Answers
Step 1
The domain refers to all values that go into a function. The range refers to all the values that come out.
Step 2
Find the domain
[tex]D=\mleft\lbrace2007,2008,2009\mright\rbrace[/tex]Step 3
Find the range
[tex]R=\mleft\lbrace234300,213200,\text{ 212,200}\mright\rbrace[/tex]m varies directly with n. Determine m when n=8 and k= 16
Answers
We have that m varies directly with n, then:
[tex]m=kn[/tex]now, if n =8 and k=16, then:
[tex]\begin{gathered} m=(16)(8)=128 \\ m=128 \end{gathered}[/tex]therefore, m = 128
b) The slope of a line is 3. The line contains the points (-1,8), and (x, 2).Then x =
Answers
The slope between two points (x1,y1) and (x2,y2) is given by:
[tex]m=\frac{y_2-y_1}{x_2-x_1}[/tex]Plugging the values of the points given and the slope we have that:
[tex]\begin{gathered} \frac{2-8}{x-(-1)}=3 \\ \frac{-6}{x+1}=3 \\ 3(x+1)=-6 \\ x+1=-\frac{6}{3} \\ x+1=-2 \\ x=-2-1 \\ x=-3 \end{gathered}[/tex]Therefore x=-3
A new cell tower is being constructed and needs a guy-wire connected 137 feet up the tower and it needs to make an angle of 56° with the ground. What length does the wire need to be?
Answers
How would I figure out 4 could you draw it out so I could understand betters it’s my first day learning this
Answers
Question 4
The sketch of the isosceles right triangle is given below
For an isosceles right triangle, the two legs are equal
So we will get the value x as follow
[tex]\begin{gathered} x^2+x^2=8^2 \\ 2x^2=8^2 \\ 2x^2=64 \\ x^2=32 \\ x=4\sqrt[]{2} \end{gathered}[/tex]The perimeter of the triangle can be obtained as follow
The perimeter is simply the sum of all the sides of the triangle
[tex]\begin{gathered} \text{Perimeter}=x+x+8 \\ \text{Perimeter}=4\sqrt[]{2}+4\sqrt[]{2}+8=8\sqrt[]{2}+8 \\ \text{Perimeter}=8\sqrt[]{2}+8 \\ \text{Perimeter}=8(\sqrt[]{2}+1) \\ \text{Perimeter}=19.31\text{ units} \end{gathered}[/tex]To get the area of the triangle
we will use the formula
[tex]\begin{gathered} \text{Area}=\frac{1}{2}\times base\times\text{height} \\ \text{Area}=\frac{1}{2}\times4\sqrt[]{2}\times4\sqrt[]{2} \\ \text{Area}=2\sqrt[]{2}\times4\sqrt[]{2} \\ \text{Area}=2\times4\times2 \\ \text{Area}=16 \end{gathered}[/tex]The area of the triangle is 16 square units
I need help finding which two could be differences of perfect cubes
Answers
Solution:
The differences of perfect cube is expressed in the form:
[tex](a)^3-(b)^3[/tex]From the given options, we have the difference of perfect cubes to be
[tex]\begin{gathered} 216a^6-27y^3\Rightarrow\left(6a^2\right)^3-\left(3y\right)^3 \\ \\ 8a^{15}-27\Rightarrow(2a^5)^3-(3)^3 \end{gathered}[/tex]Hence, the correct options are
Hi I need help with these problems only 1 and 3 since my teacher told us to do even number and if I don't know what to do at all
Answers
Since we are dealing with a right triangle, we can use the following trigonometric identities
[tex]\sin \theta=\frac{O}{H},\cos \theta=\frac{A}{H}[/tex]Where θ is an inner angle (different than 90°) of the triangle, O is the opposite side to θ, A is the adjacent side to θ, and H is the hypotenuse.
a) In our case,
[tex]\begin{gathered} \theta=30\text{degre}e \\ H=14,A=m,O=n \\ \Rightarrow\sin (30degree)=\frac{n}{14} \\ \Rightarrow n=14\cdot\sin (30degree)=14\cdot0.5=7 \\ \Rightarrow n=7 \end{gathered}[/tex]and
[tex]\begin{gathered} \Rightarrow\cos (30degree)=\frac{m}{14} \\ \Rightarrow m=14(\cos (30degree))=14\cdot\frac{\sqrt[]{3}}{2}=7\sqrt[]{3} \\ \Rightarrow m=7\sqrt[]{3} \end{gathered}[/tex]The answers are n=7 and m=7sqrt(3).
3) In a diagram, the problem states
Using the same trigonometric identities mentioned in part 1) (plus the tangent function), we get
[tex]\begin{gathered} \sin (30degree)=\frac{18}{H},\tan (30degree)=\frac{18}{A} \\ \Rightarrow H=\frac{18}{\sin(30degree)},A=\frac{18}{\tan(30degree)}=\frac{18}{\frac{1}{\sqrt[]{3}}}=18\sqrt[]{3} \\ \Rightarrow H=\frac{18}{0.5}=36,A=18\sqrt[]{3} \\ \Rightarrow H=36,A=18\sqrt[]{3} \end{gathered}[/tex]The hypotenuse is equal to 36 ft, and the other leg is equal to 18sqrt(3) ft
11) Find the Constant of proportionality (k) from the equations below.
Answers
Direct variation is in the form
y = kx
a y = 7x the constant k is 7
b y = 12x the constant k is 12
c y = 1/2x the constant k is 1/2
d y = -4x the constant k is -4
If there are 2.54 cm in 1 inch, how long in inches is a meter stick?
Answers
To solve the exercise, we can use the rule of three:
Since we know that there are 100 centimeters in a meter, we have:
[tex]\begin{gathered} 2.54\operatorname{cm}\rightarrow1\text{ in} \\ 100\operatorname{cm}\rightarrow x\text{ in} \end{gathered}[/tex][tex]\begin{gathered} x=\frac{100\operatorname{cm}\cdot1in}{2.54\operatorname{cm}} \\ x=\frac{10in\cdot1}{2.54} \\ x=\frac{10in}{2.54} \\ x=39.37in \end{gathered}[/tex]Therefore, there are 39.37 inches in a meter stick.
Use the graph to complete the statements.For every dollar you spend, you can getpounds of grapes.For each pound of grapes, you would need $
Answers
We are given a graph of pounds of grapes vs dollar spent.
To know what $1 worth of grapes is, we go to the horizontal axis to locate 1 and trace up to where it meets up with the graph and on getting that point on the graph, we trace it left to the vertical axis to get $0.5 (50 cent)
To get the dollars' worth for each grape, we locate one on the vertical axis and trace it right to where it cuts the graph. This can easily be seen to
You need to ride an average of at least 35 miles per day for five consecutive days toqualify for a cross-country biking expedition. The distances (in miles) of your rides in thefirst four days are 45, 33, 27, and 26. What distances on the fifth day will allow you toqualify for the competition?
Answers
We are to maintain a constant mean distance of ( d-avg ) to qualify for the cross-country biking expedition.
The qualification for the expedition is to rirde an average distance of:
[tex]d_{avg}\text{ }\ge\text{ 35 miles each for 5 consecutive day }[/tex]We are already on target for 4 days. For which we covered a distance ( d ) for each day:
[tex]\begin{gathered} \text{\textcolor{#FF7968}{Day 1:}}\text{ 45 miles} \\ \text{\textcolor{#FF7968}{Day 2:}}\text{ 33 miles} \\ \text{\textcolor{#FF7968}{Day 3:}}\text{ 27 miles} \\ \text{\textcolor{#FF7968}{Day 4: }}\text{26 miles} \end{gathered}[/tex]We are to project how much distance we must cover atleast on the fifth day ( Day 5 ) so that we can qualify for the expedition. The only condition for qualifying is given in terms of mean distance traveled over 5 days.
The mean value of the distance travelled over ( N ) days is expressed mathematically as follows:
[tex]d_{avg}\text{ =}\sum ^N_{i\mathop=1}\frac{d_i}{N}[/tex]Where,
[tex]\begin{gathered} d_i\colon Dis\tan ce\text{ travelled on ith day} \\ N\colon\text{ The total number of days in consideration} \end{gathered}[/tex]We have the data available for the distance travelled for each day ( di ) and the total number of days in consideration ( N = 5 days ). We will go ahead and used the standard mean formula:
[tex]d_{avg}\text{ = }\frac{d_1+d_2+d_3+d_4+d_5}{5}[/tex]Then we will apply the qualifying condtion to cover atleast 35 miles for each day for the course of 5 days.
[tex]\frac{45+33+27+26+d_5}{5}\ge\text{ 35}[/tex]Then we will solve the above inequality for Day 5 - (d5) as follows:
[tex]\begin{gathered} d_5+131\ge\text{ 35}\cdot5 \\ d_5\ge\text{ 175 - 131} \\ \textcolor{#FF7968}{d_5\ge}\text{\textcolor{#FF7968}{ 44 miles}} \end{gathered}[/tex]The result of the above manipulation shows that we must cover a distance of 44 miles on the 5th day so we can qualify for the expedition! So the range of distances that we should cover atleast to qualify is:
[tex]\textcolor{#FF7968}{d_5\ge}\text{\textcolor{#FF7968}{ 44 miles}}[/tex]All covered distances greater than or equal to 44 miles will get us qualified for the competition!
2. A certain elevator can hold a maximum weight of 2,800 pounds. This total is determined by estimating the average adult weight as 200 pounds and the average child weight as 80 pounds. Write an inequality that represents this situation, then graph it on the coordinate plane below. Determine a combination of children, c, and adults, a, that can safely ride the elevator.
Answers
Let's begin by listing out the given information
Elevator Max weight (e) = 2000 lb
Each adult's weight (a) = 200 lb
Each child's weight (c) = 80 lb
Our inequality is given by:
[tex]200a+80c\le2000-----1[/tex]We will proceed to find the combination of people that can safely ride the elevator
[tex]\begin{gathered} 200a+80c\le2000 \\ \text{If there are 5 a}dults,\text{ we have:} \\ 200(5)+80c\le2000 \\ 1000+80c\le2000 \\ 80c\le2000-1000 \\ 80c\le1000 \\ c\le12.5(\text{that's 12 }children) \\ \text{If there are 8 a}dults,\text{ we have:} \\ 200(8)+80c\le2000 \\ 80c\le2000-1600 \\ 80c\le400 \\ c\le5(\text{5 }children) \end{gathered}[/tex]Let f(-1)=16 and f(5) = -8a. Find the distance between these pointsb. Find the midpoint between these pointsc. Find the slope between these points
Answers
We are given the following information
f(-1) = 16 and f(5) = -8
Which means that
[tex](x_1,y_1)=(-1,16)\text{and}(x_2,y_2)=(5,-8)[/tex]a. Find the distance between these points
Recall that the distance formula is given by
[tex]d=\sqrt[]{\mleft({x_2-x_1}\mright)^2+\mleft({y_2-y_1}\mright)^2}[/tex]Let us substitute the given points into the above distance formula
[tex]\begin{gathered} d=\sqrt[]{({5_{}-(-1)})^2+({-8_{}-16_{}})^2} \\ d=\sqrt[]{({5_{}+1})^2+({-24_{}})^2} \\ d=\sqrt[]{({6})^2+({-24_{}})^2} \\ d=\sqrt[]{36^{}+576^{}} \\ d=\sqrt[]{612} \end{gathered}[/tex]Therefore, the distance between these points is √612 = 24.738
b. Find the midpoint between these points
Recall that the midpoint formula is given by
[tex](x_m,y_m)=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})[/tex]Let us substitute the given points into the above midpoint formula
[tex]\begin{gathered} (x_m,y_m)=(\frac{-1_{}+5_{}}{2},\frac{16_{}+(-8)_{}}{2}) \\ (x_m,y_m)=(\frac{-1_{}+5}{2},\frac{16_{}-8}{2}) \\ (x_m,y_m)=(\frac{4}{2},\frac{8}{2}) \\ (x_m,y_m)=(2,4) \end{gathered}[/tex]Therefore, the midpoint of these points is (2, 4)
c. Find the slope between these points
Recall that the slope is given by
[tex]m=\frac{y_2−y_1}{ x_2−x_1}[/tex]Let us substitute the given points into the above slope formula
[tex]m=\frac{-8-16}{5-(-1)}=\frac{-24}{5+1}=\frac{-24}{6}=-4[/tex]Therefore, the slope of these points is -4.
Find the equation of a line that contains the point (-2, -6) is perpendicular to the line
Answers
Answer:
answer Is y= 5x+4......