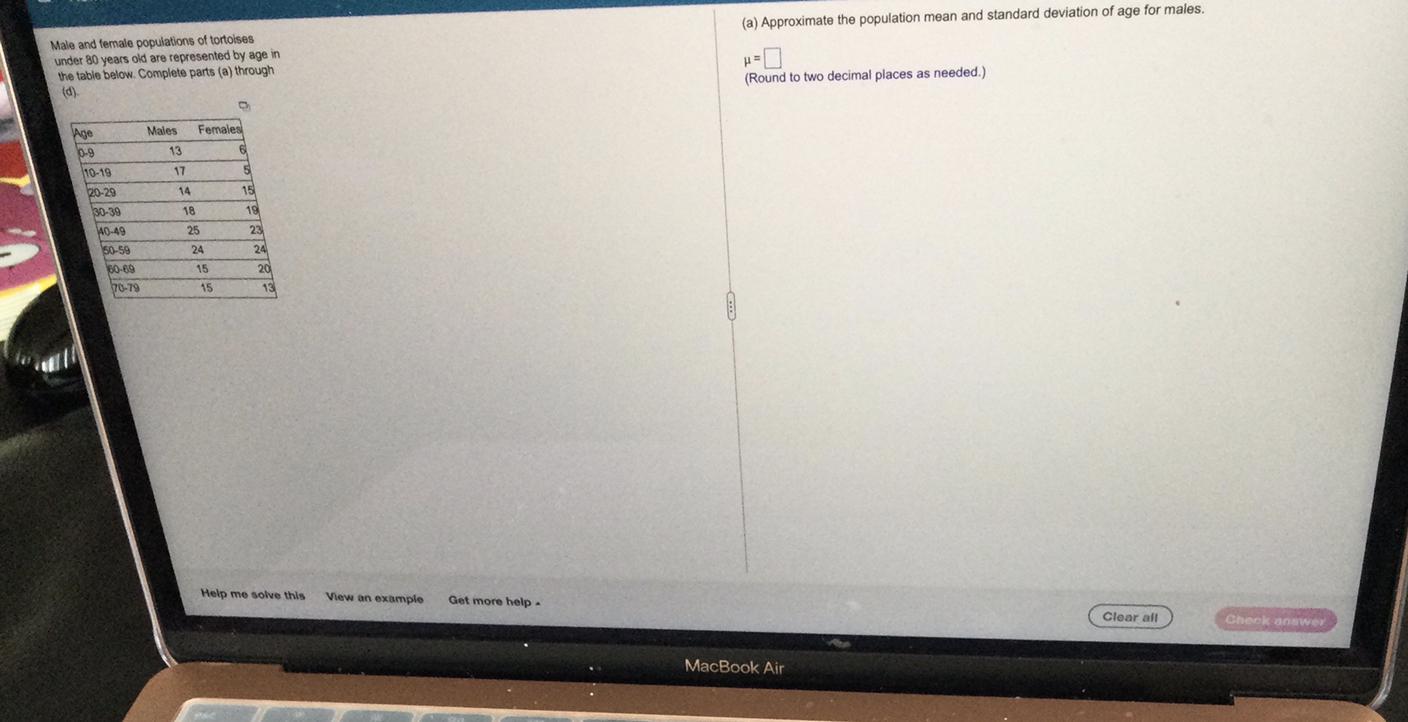
(a) Approximate the population mean and standard deviation of age for malesMale and female populations of totunder 10 years old are represented by age inthe table below. Completo port(a) through10(Round to two decimal places as needed)
Answers
Answer:
Step-by-step explanation:
The population means is an average of a group characteristic. A characteristic is just an item of interest.
[tex]\begin{gathered} \mu=\frac{\sum ^{}_{}x}{N} \\ \mu=\frac{\text{Sum of all the items}}{\text{ Number of items}} \end{gathered}[/tex]Then, for the population mean and standard deviation of the age for males;
Total of population: 266
[tex]undefined[/tex]Related Questions
Determine the number of solutions for the following system of linear equations. If there is only onesolution, find the solution.x + 3y – 2z = 6- 4x - 7y + 3z = 3- 7x – 4y - 3z = -5AnswerKeypadKeyboard ShortcutsSelecting an option will enable input for any required text boxes. If the selected option does not have anyassociated text boxes, then no further input is required.O No SolutionO Only One SolutionX =y =Z=Infinitely Many Solutions
Answers
First, let's clear z from equation 1:
[tex]\begin{gathered} x+3y-2z=6\rightarrow x+3y-6=2z \\ \rightarrow z=\frac{1}{2}x+\frac{3}{2}y-3 \end{gathered}[/tex]Now, let's plug it in equations 2 and 3, respectively:
[tex]\begin{gathered} -4x-7y+3z=3 \\ \rightarrow-4x-7y+3(\frac{1}{2}x+\frac{3}{2}y-3)=3 \\ \\ \rightarrow-4x-7y+\frac{3}{2}x+\frac{9}{2}y-9=3 \\ \\ \rightarrow-\frac{5}{2}x-\frac{5}{2}y=12_{} \\ \end{gathered}[/tex][tex]\begin{gathered} -7x-4y-3z=-5 \\ \rightarrow-7x-4y-3(\frac{1}{2}x+\frac{3}{2}y-3)=-5 \\ \\ \rightarrow-7x-4y-\frac{3}{2}x-\frac{9}{2}y+3=-5 \\ \\ \rightarrow-\frac{17}{2}x-\frac{17}{2}y=-8 \end{gathered}[/tex]We'll have a new system of equations:
[tex]\begin{gathered} -\frac{5}{2}x-\frac{5}{2}y=12_{} \\ \\ -\frac{17}{2}x-\frac{17}{2}y=-8 \end{gathered}[/tex]Now, let's simplify each equation. To do so, we'll multiply the first one by -2/5 and the second one by -2/17. We'll get:
[tex]\begin{gathered} x+y=-\frac{24}{5} \\ \\ x+y=\frac{16}{17} \end{gathered}[/tex]Now, let's solve each equation for y to see them as a pair of line equations:
[tex]\begin{gathered} y=-x-\frac{24}{5}_{} \\ \\ y=-x+\frac{16}{17} \end{gathered}[/tex]Notice that this lines have the same slope. Therefore, they're parallel and do not intercept.
This way, we can conlcude that the original system has no solution.
Select the correct answer.What are the asymptote and the y-intercept of the function shown in the graph?
Answers
Answer:
Explanation:
Here, we want to get the y-intercept and the asymptote of the shown function
The y-intercept is simply the point at which the curve crosses the y-axis
We can see this at the point y = 5 which is coordinate form is (0,5)
The asymptote is the point on the y-axis where the curve almost flattens out but will never touch
We have this at the point y = 2
There is a bag full of 30 different colored and/or patterned balls. How many different three ball combinations can you have if you pull three balls out of the bag?Part 2: Write down (in factorial form) the total number of possible combinations there are if you draw all the balls out of the bag one at a time.I am really stuck on part 2
Answers
a) 4060 different combinations
b) 30!
Explanation:Given:
Total balls of different patterns = 30
To find:
a) the different three-ball combinations one can have if 3 balls are pulled out of the bag
b) the total number of possible combinations there are if you draw all the balls out of the bag one at a time in factorial form
a) To determine the 3-ball combinations, we will apply combination as the order they are picked doesnot matter
[tex]\begin{gathered} for^^^\text{ the 3 ball comination = }^nC_r \\ where\text{ n = 30, r = 3} \\ \\ ^{30}C_3\text{ = }\frac{30!}{(30-3)!3!} \\ ^{30}C_3\text{ = }\frac{30!}{27!3!}\text{= }\frac{30\times29\times28\times27!}{27!\times3\times2\times1} \\ \\ ^{30}C_3\text{ = 4060 different combinations} \end{gathered}[/tex]b) if you are to draw all the balls one at a time, then for the 1st it will be 30 possibilities, the next will reduce by 1 to 29 possibilities, followed by 28 possibilities, etc to the last number 1
The possible combination = 30 × 29 × 28 × 27 × 26 × 25 ......5 × 4 × 3 × 2 ×1
The above is an expansion of a number factorial. the number is 30
30! = 30 × 29 × 28 × 27 × 26 × 25 ......5 × 4 × 3 × 2 ×1
Hence, the total number of possible combinations when you draw all the balls out of the bag one at a time in factorial form is 30!
3 3/10 divied by 1 4/7 in lowest terms
Answers
Answer:
Step-by-step explanation:
The answer is [tex]\frac{21}{10}[/tex] or 2 [tex]\frac{1}{10}[/tex] or 2.1.
Depending on what form your answer needs to be in, it can be one of those.
Explanation:
Turn both the mixed numbers into improper fractions. To do this, take the outside number and multiply it by the denominator. Then, add that number to the numerator. For this specific question, you would take 3×10 (because 10 is the denominator) and add it to the numerator, 3, giving the improper fraction [tex]\frac{33}{10}[/tex]. Doing the same to the divisor, you would get [tex]\frac{11}{4}[/tex].Next, take the divisor ([tex]\frac{11}{7}[/tex]) and turn it into the reciprocal ("flip" the fraction), making it [tex]\frac{7}{11}[/tex].Now, simply multiply the dividend ([tex]\frac{33}{10}[/tex]) to the reciprocal of the divisor ([tex]\frac{4}{11}[/tex]).So, your new equation is a much easier [tex]\frac{33}{10}[/tex]×[tex]\frac{7}{11}[/tex]=[tex]\frac{231}{110}[/tex]. These both are reducable by 11, therefore giving you the final answer of [tex]\frac{21}{10}[/tex].
Note: Upon reaching this step, you can simplify 33 into 3×11, then divide out the 11 from the numerator and the denominator making it a much easier problem to simplify. Hope this helps!
1 Factor each polynomial over the set of realC)f(x) = x^4- 25x^2 + 144
Answers
Notice that:
[tex]\begin{gathered} x^4-25x^2+144=(x^2)^2+(-9-16)x^2+(-9)(-16) \\ =(x^2-9)(x^2-16)\text{.} \end{gathered}[/tex]Now, notice that:
[tex]\begin{gathered} x^2-9=x^2-3^2=(x+3)(x-3), \\ x^2-16=x^2-4^2=(x+4)(x-4)\text{.} \end{gathered}[/tex]Therefore:
[tex]x^4-25x^2+144=(x+3)(x-3)(x+4)(x-4)\text{.}[/tex]Answer:
[tex]x^4-25x^2+144=(x+3)(x-3)(x+4)(x-4)\text{.}[/tex]
a) which is equation of the parabola? b) name the focus and directrix ? c) name vertex and axis of symmetry?
Answers
The equation of the parabola whose axis of symmetry is parallel to x-axis is
[tex](y-k)^2=4p(x-h)[/tex]where the focus is
[tex]\text{focus}=(h+p,k)[/tex]and the directrix is
[tex]x=h-p[/tex]In our case, the focus is (6,1) and the directrix is x =2; therefore, we have
[tex](6,1)=(h+p,k)[/tex]and
[tex]h-p=2[/tex]These equations give
[tex]k=1,h=4,p=2[/tex]Hence, the equation of the parabola is
[tex](y-1)^2=8(x-4)[/tex]Graph the equation after plotting at least three points. Y= -2/3x+4
Answers
Given the function:
[tex]y=-\frac{2}{3}x+4[/tex]It's required to graph the function by joining at least 3 points.
Let's select the points x = -3, x = 3, and x = 9.
Substituting x = -3:
[tex]y=-\frac{2}{3}\cdot(-3)+4[/tex]Operating:
[tex]\begin{gathered} y=-\frac{-6}{3}+4 \\ y=2+4 \\ y=6 \end{gathered}[/tex]The first point is (-3,6)
Substitute x = 3:
[tex]y=-\frac{2}{3}\cdot3+4[/tex]Calculating:
[tex]\begin{gathered} y=-\frac{6}{3}+4 \\ y=-2+4 \\ y=2 \end{gathered}[/tex]The second point is (3,2)
Now for x = 9:
[tex]\begin{gathered} y=-\frac{2}{3}\cdot9+4 \\ y=-\frac{18}{3}+4 \\ y=-6+4 \\ y=-2 \end{gathered}[/tex]The third point is (9,-2).
Plotting the three points and joining them with a line, we get the following graph:
Use the drawing tool(s) to form the correct answer on the provided graph.
Graph the solution to this system of inequalities in the coordinate plane.
3y>2x + 122x + y ≤ -5Having trouble rewriting in form. Graphing once in form okay.
Answers
Explanation
We are given the following system of inequalities:
[tex]\begin{gathered} 3y>2x+12 \\ 2x+y\leqslant-5 \end{gathered}[/tex]We are required to graph the given system of inequalities.
This is achieved thus:
- First, we determine two coordinates from the given inequalities:
[tex]\begin{gathered} 3y>2x+12 \\ \text{ Suppose }3y=2x+12 \\ \text{ Let x = 0} \\ 3y=12 \\ y=4 \\ Coordinate:(0,4) \\ \\ \text{Suppose }3y=2x+12 \\ \text{ Let y = 0} \\ 0=2x+12 \\ 2x=-12 \\ x=-6 \\ Coordinate:(-6,0) \end{gathered}[/tex]- Now, we plot the points on a graph. Since the inequality is "strictly greater than", the line drawn will be broken. The graph is shown below:
- Using the second inequality, we have:
[tex]\begin{gathered} 2x+y\leqslant-5 \\ \text{ Suppose }2x+y=-5 \\ \text{ Let y = 0} \\ 2x=-5 \\ x=-2.5 \\ Coordinate:(-2.5,0) \\ \\ \text{Suppose }2x+y=-5 \\ \text{ Let x = 0} \\ y=-5 \\ Coordinate:(0,-5) \end{gathered}[/tex]The graph becomes:
Combining both graphs, we have the solution to be:
The solution is the intersection of both graphs as indicated above.
For z1 = 9cis 5pi/6 and z2=3cis pi/3, find z1/z2 in rectangular form
Answers
We have the following:
are the complex number
[tex]\begin{gathered} z_1=9cis\frac{5\pi}{6}_{} \\ z_2=3\text{cis}\frac{\pi}{3} \\ \frac{z_1}{z_2} \end{gathered}[/tex]So magnitudes are r₁ = 9, and r₂ = 3 and arguments are ∅₁ = 5π/6, and ∅₂ = π/3
[tex]\frac{z_1}{z_1}=\frac{r_1}{r_2}\cdot\text{cis(}\emptyset_1\cdot\emptyset_{2})[/tex]replacing:
[tex]\begin{gathered} \frac{z_1}{z_2}=\frac{9}{3}\cdot\text{cis}(\frac{5\pi}{6}-\frac{\pi}{3}) \\ \frac{z_1}{z_2}=3\cdot\text{cis}(\frac{5\pi}{6}-\frac{2\pi}{6}) \\ \frac{z_1}{z_2}=3\cdot\text{cis}(\frac{3\pi}{6}) \\ \frac{z_1}{z_2}=3\cdot\text{cis}(\frac{\pi}{2})\rightarrow\text{cis}(\frac{\pi}{2})=\cos \mleft(\frac{\pi}{2}\mright)+3i\sin \mleft(\frac{\pi}{2}\mright) \\ \frac{z_1}{z_2}=3\cdot\lbrack\cos (\frac{\pi}{2})+i\sin (\frac{\pi}{2})\rbrack \\ \frac{z_1}{z_2}=3\cdot\lbrack0+i\cdot1)\rbrack \\ \frac{z_1}{z_2}=3\cdot0+3\cdot i \\ \frac{z_1}{z_2}=3i \end{gathered}[/tex]Therefore, the answer is option D 3i
1. find the sum of the first 7 terms of the following sequence round to the nearest hundredth if necessary 18,-6,22. Find the sum of the first 6 terms of the following sequence to the nearest hundredth:324, 54, 9
Answers
You can find the sum of the first n terms of a geometric sequence using the formula:
[tex]S_n=\frac{a_1(1-r^n)}{1-r}[/tex]1. First, let's calculate r:
[tex]\begin{gathered} r_1=18-(-6)=24 \\ r_2=-6-2=-8 \\ r=-\frac{8}{24}=-\frac{1}{3} \end{gathered}[/tex]Replacing the values in the formula, (n=7 , r=-1/3) we get that:
[tex]S_n=13.51[/tex]2. Let's calculate r:
[tex]\begin{gathered} r_1=324-54=270 \\ r_2=54-9=45 \\ r=\frac{r_2}{r_1}=\frac{45}{270}=\frac{1}{6} \end{gathered}[/tex]Using the formula with the data we have, (n=6 , r=1/6) we get that
[tex]S_n=388.79[/tex]can you help me is it < > or =
Answers
The correct answer is
[tex]\frac{1}{4}\times4\frac{1}{2}<4\frac{1}{2}[/tex]Each vertical cross-section of the triangular prism shown below is an isosceles triangle.4What is the slant height, s, of the triangular prism?Round your answer to the nearest tenth.The slant height isunits
Answers
The length of the diagonal of a cube can be calculated by the formula
[tex]\begin{gathered} d=a\sqrt[]{3} \\ \text{where a is one side of the cube} \\ a=60 \end{gathered}[/tex]Hence,
[tex]\begin{gathered} d=60\sqrt[]{3}\text{ units} \\ d=103.92\text{ units (2 decimal place)} \end{gathered}[/tex]x^2+x^2=11.3^2 solve using the pathogen theorem
Answers
The value of x in the given expression is 8.
What is Pythagoras theorem?Pythagorean theorem, the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (a² + b² = c²).
Given an expression, x²+x² = 11.3²
2x² = 11.3²
[tex]\sqrt{2}[/tex]x = 11.3
x = 7.99 = 8
Hence, The value of x in the given expression is 8.
For more references on Pythagorean theorem, click;
https://brainly.com/question/14930619
#SPJ1
Simplify each expression by using The Distributive Property and combine like terms to simplify the expression.4(3х - 2)
Answers
The given expression is
[tex]undefined[/tex]There are 364 people That have to go from the airport to the hotel. One sand can’t transfer 12 people have any vans are needed
Answers
To find the number of van that are needed you divide the number of people into the people that a van can transport:
As the result of division is a decimal number you approximate it to the next whole number (because you can not have 0.33 of a van)
Then, there are needed 31 vans2x^3 - 4x^2 - 50x + 100 factoring completely
Answers
The factor is 2(x−2)(x+5)(x−5).
From the question, we have
2x³−4x²−50x+100
=2(x−2)(x+5)(x−5)
Factors :
The positive integers that can divide a number evenly are known as factors in mathematics. Let's say we multiply two numbers to produce a result. The product's factors are the number that is multiplied. Each number has a self-referential element. There are several examples of factors in everyday life, such putting candies in a box, arranging numbers in a certain pattern, giving chocolates to kids, etc. We must apply the multiplication or division method in order to determine a number's factors.The numbers that can divide a number exactly are called factors. There is therefore no residual after division. The numbers you multiply together to obtain another number are called factors. A factor is therefore another number's divisor.
To learn more about factors visit: https://brainly.com/question/20293447
#SPJ9
Select the correct choice below and fill in the answer
Answers
Step 1:
Write the function
[tex]g(x)=x^5-16x^3[/tex]Step 2:
Write an inequality equation where g(x) > 0
[tex]\begin{gathered} x^5-16x^3\text{ > 0} \\ \text{Factorize the left hand side of the equation} \\ x^3(x^2\text{ - 16) > 0} \\ x^3(x\text{ - 4)(x + 4) > 0} \end{gathered}[/tex]Step 3:
Identify the intervals
- 4 < x < 0 or x > 4
[tex]\text{Answer in interval notation: }(\text{ - 4 , 0 ) }\cup\text{ ( 4 , }\infty\text{ )}[/tex]A bag of fertilizer covers 2,000 square feet of lawn. Find how many bags of fertilizer should be purchased to cover a rectangular lawn that is 29400 square feet.
Answers
Okay, here we have this:
Considering the provided information, we are going to calculate how many bags of fertilizer should be purchased to cover a rectangular lawn that is 29400 square feet, so we obtain the following:
Number of bags=Total space / Space per bag
Number of bags=29400ft² / 2000ft²
Number of bags=14.7
Number of bags≈15 bags of fertilizer.
Finally we obtain that rounded to the nearest unit, 15 bags of fertilizer are needed.
Using the image above, which of the following are opposite rays?A QP and PLB PL and PQC LP and QPD LQ and PQ
Answers
ANSWER
PL and PQ
EXPLANATION
We want to find which of the rays are opposite rays.
That means which of the rays are going in opposite direction and are the same length to one another.
We see different rays in the image. Some are going upward while some are going downward.
The ones going upward are:
LQ and PQ
The ones going downward are:
QL and PL
By observation, among all the options, we see that only PL and PQ are the same length and that are in opposite directions.
That means that the answer is PL and PQ
Given: CD⎯⎯⎯⎯⎯⎯ is an altitude of △ABC.Prove: a2=b2+c2−2bccosAFigure shows triangle A B C. Segment A B is the base and contains point D. Segment C D is shown forming a right angle. Segment C D is labeled h. Segment A B is labeled c. Segment B C is labeled a. Segment A C is labeled b. Segment A D is labeled x. Segment D B is labeled c minus x. Select from the drop-down menus to correctly complete the proof.Statement ReasonCD⎯⎯⎯⎯⎯⎯ is an altitude of △ABC. Given△ACD and △BCD are right triangles. Definition of right trianglea2=(c−x)2+h2a2=c2−2cx+x2+h2Square the binomial.b2=x2+h2cosA=xbbcosA=xMultiplication Property of Equalitya2=c2−2c(bcosA)+b2a2=b2+c2−2bccosA Commutative Properties of Addition and Multiplication
Answers
Solution:
The equation below is given as
[tex]a^2=(c-x)^2+h^2[/tex]This represents the
PYTHAGOREAN THEOREM
The second equation is given below as
[tex]b^2=x^2+h^2[/tex]This represents the
PYTHAGOREAN THEOREM
The third expression is given below as
[tex]\cos A=\frac{x}{b}[/tex]This represents
Definition of cosine
The fourth expression is given below as
[tex]a^2=c^2-2c(bcosA)+b^2[/tex]This represents
Substitution property of equality
Which equation is true when the value of x is -12
Answers
We are told to check for the correct equation that satisfies when the value of x = -12.
Let us resolve that by picking one of the options and testing it to confirm if it satisfies the value of x = -12.
Starting with OPTION B
[tex]15-\frac{1}{2}x=21[/tex]Solve for x
Subtract 12 from both sides
[tex]\begin{gathered} 15-15-\frac{1}{2}x=21-15 \\ -\frac{1}{2}x=6 \end{gathered}[/tex]Multiply both sides by 2
[tex]\begin{gathered} 2\times-\frac{1}{2}x=2\times6 \\ -1x=12 \end{gathered}[/tex]Divide both sides by -1
[tex]\begin{gathered} \frac{-1x}{-1}=\frac{12}{-1} \\ x=-12 \end{gathered}[/tex]From the solution, we can conclude that the above equation is true when the value of x = -12.
The correct option is Option B.
i have to use interval notation and i’m stuck on it
Answers
Given two sets of real numbers:
[tex]\begin{gathered} D=\mleft\lbrace w\mright|w\ge4\} \\ E=\mleft\lbrace w\mright|w<8\} \end{gathered}[/tex]we will write the given sets as intervals
so,
[tex]\begin{gathered} D=\lbrack4,\infty) \\ E=(-\infty,8) \end{gathered}[/tex]The intersections and the union of the sets will be as follows:
[tex]\begin{gathered} D\cap E=\lbrack4,8) \\ \\ D\cup E=(-\infty,\infty) \end{gathered}[/tex]Find the formula for an exponential equation that passes through the points, (0,5) and (1,2). The exponential equation should be of the form y = ab^x
Answers
Answer:
[tex]y=5\cdot(\frac{2}{5})^x[/tex]Explanation:
The exponential equation has the form
[tex]y=a\cdot b^x[/tex]Since it passes through the point (0, 5). Let's replace (x, y) by (0, 5) to find the value of a
[tex]\begin{gathered} 5=a\cdot b^0 \\ 5=a\cdot1 \\ 5=a \end{gathered}[/tex]Then, the equation is
[tex]y=5\cdot b^x[/tex]To find the value of b, we will use the point (1, 2), so replacing x = 1 and y = 2, we get:
[tex]\begin{gathered} 2=5\cdot b^1 \\ 2=5\cdot b \\ \frac{2}{5}=\frac{5\cdot b}{5} \\ \frac{2}{5}=b \end{gathered}[/tex]Then, the exponential equation is:
[tex]a=5\cdot(\frac{2}{5})^x[/tex]Answer:
Step-by-step explanation: the answer is a= 5(2/5)^x
8+7i/4-6iI need the answer and how to solve asap!
Answers
ANSWER
[tex]\frac{1}{52}(-10\text{ + 76i) or }\frac{1}{26}(-5\text{ + 38i)}[/tex]EXPLANATION
We are given the fraction of complex numbers:
[tex]\frac{\text{8 + 7i}}{4\text{ - 6i}}[/tex]To simplify this, we will find the conjugate of the denominator and then multiply that with the numerator and denomiator.
The conjugate is gotten by changing the sign of the denominator. That is:
4 + 6i
So, we have:
[tex]\begin{gathered} \frac{\text{8 + 7i}}{4\text{ - 6i}}\cdot\text{ }\frac{4\text{ + 6i}}{4\text{ + 6i}} \\ =\text{ }\frac{(8\text{ + 7i) (4 + 6i)}}{(4\text{ - 6i) (4 + 6i)}} \\ =\frac{(8\cdot\text{ 4) + (8 }\cdot\text{ 6i) + (7i }\cdot\text{ 4) + (7i }\cdot\text{ 6i)}}{(4\cdot\text{ 4) + (6i }\cdot\text{ 4) - (6i }\cdot\text{ 4) - (6i }\cdot\text{ 6i)}} \\ We\text{ know that i = }\sqrt{i},\text{ so i }\cdot\text{ i = -1:} \\ \Rightarrow\text{ }\frac{\text{ }32\text{ + 48i + 28i - 42}}{16\text{ + 24i - 24i + 36}} \\ =\text{ }\frac{-10\text{ + 76i}}{16\text{ + 36}}\text{ = }\frac{-10\text{ + 76i}}{52} \\ =\text{ }\frac{1}{52}(-10\text{ + 76i) or }\frac{1}{26}(-5\text{ + 38i)} \end{gathered}[/tex]That is the answer.
is the least common denominator of two fractions always greater than the denominators of the fractions
Answers
The least common denominator of two fractions is not always greater than the denominators of each fraction because sometimes the least common denominator is equal to the greater denominator. For example, if we have the fractions
[tex]\frac{4}{5}-\frac{1}{5}[/tex]In this case, since you have equal denominators, the least common factor would be 5, not greater than 5.
Another example could be
[tex]4+\frac{2}{9}[/tex]In this case, the least common denominator is 9, not greater than 9.
Therefore, the least common denominator is not always greater than the denominator of the fractions.a figure has vertices (-13,13), (26,52), (39,39) what would the new coordinates of the vertices to the nearest tenth if the image were reduced by a scale factor of 0.77 with the origin as the center of dilation
Answers
Explanation
Given that the figure has vertices (-13,13), (26,52), (39,39), to reduce the image by a scale factor of 0.77 with the origin as the center of dilation, we will multiply the x and y coordinates by the scale factors.
8i+ 5 - 2i equals 3i+ 23
Answers
We will have:
[tex]8i+5-2i=3i+23[/tex]We will operate like terms and solve for i, that is:
[tex]8i-2i-3i=23-5\Rightarrow3i=18\Rightarrow i=6[/tex]*Step by step:
[tex]8i+5-2i=3i+23\Rightarrow6i+5=3i+23[/tex][tex]\Rightarrow6i+5-5=3i+23-5\Rightarrow6i=3i+18[/tex][tex]\Rightarrow6i-3i=3i+18-3i\Rightarrow3i=18[/tex][tex]\Rightarrow\frac{3}{3}i=\frac{18}{3}\Rightarrow i=6[/tex]Tomas is leaving a tip of 18% of his original bill. If the amount of the tip is $2.34, which of the following equations can be used to find the amount of his original bill?0.18b = 2.34b - 0.18 = 2.342.34 x 0.18 = bb/2.34 = 0.18
Answers
Answer
0.18b = 2.34
Step-by-step explanation
Let's call b to the bill
The tip is 18% of the bill. To find the 18 percent of a number, we need to multiply this number by 18 and then divide by 100. In this case, the tip is:
[tex]\begin{gathered} tip=\frac{18}{100}b \\ tip=0.18b \end{gathered}[/tex]The amount of the tip is $2.34, then:
[tex]0.18b=2.34[/tex]Given the points A(-8,-7) and B(8,5) find the coordinates of point P on directed line segment AB that partitions AB into the ratio 3:1
Answers
Given the points A(-8,-7) and B(8,5) find the coordinates of point P on directed line segment AB that partitions AB into the ratio 3:1
step 1
Find the distance in the x-coordinate between A and B
dABx=(8-(-8)=8+8=16 units
Find the distance in the y-coordinate between A and B
dABy=5-(-7)=5+7=12 units
step 2
we know that
point P on directed line segment AB that partitions AB into the ratio 3:1
so
AP/AB=3/(3+1)
AP/AB=3/4
Find the x coordinate of point P
APx/ABx=3/4
substitute
APx/16=3/4
APx=16*(3/4)
APx=12 units
The x-coordinate of P is
Px=Ax+APx
where
Ax is the x-coordinate of P
Px=-8+12=4
step 3
Find the y-coordinate of P
we have that
APy/ABy=3/4
substitute
APy/12=3/4
APy=12*(3/4)
APy=9
The y coordinate of P is
Py=APy+Ay
where
Ay is the y-coordinate of P
Py=9+(-7)=2
therefore
the answer is
The coordinate of P are (4,2)Anna found that there are 3^4 options for pizzas with different loppings at her local are there for pizzas? B. 12 c. 64 D.BA ker notes
Answers
As there are 3^4 options for pizzas, we can calculate this as:
[tex]3^4=3\cdot3\cdot3\cdot3=81[/tex]Answer: 3^4 options is equivalent to 81 options (option D).