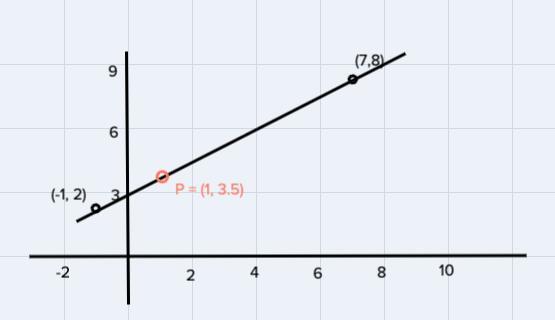
1. Given the points Al-1, 2) and B(7, 8), find the coordinates of the polnt P on the directed line segment JB that partitions AB in the ratio 1:3. Plot P along with segment AB. 10 B 6 (x,y) = (x1+k(x2 - x2),y. +k(y2-y) 2 210182632 2 68 110 2 24 6 8 -10 2. Find the coordinates of P so that P partitions AB in the ratio 5.1 with A(2, 4) and B(8, 10). L 3. Find the coordinates of P so that P partitions AB in the ratio 1 to 3 with A(-5, 4) and B(7,-4). 4. Find the coordinates of P so that P partitions AB in the ratio 3:4 with A(-9, -9) and B(5,-2).
Answers
We can find the point with help of the end points and the ratio so:
[tex]\begin{gathered} x=-1+\frac{1}{1+3}(7-(-1)) \\ x=-1+\frac{1}{4}8 \\ x=-1+2 \\ x=1 \end{gathered}[/tex]now for y:
[tex]\begin{gathered} y=2+\frac{1}{1+3}(8-2) \\ y=2+\frac{1}{4}6 \\ y=3.5 \end{gathered}[/tex]So now we can graph it so:
Related Questions
Find the equation of the normal in the form ax + by + c = 0 at the point where x = 4, for thecurve8=y = 2x2 - 4x3 - - 1х
Answers
We are given the equation of a curve;
[tex]2x^2-4x^{\frac{3}{2}}-\frac{8}{x}-1[/tex]To solve this we begin by taking the derivative of this curve. Note that the slope of this curve is its first derivative.
We now have;
[tex]\begin{gathered} \frac{d}{dx}(2x^2-4x^{\frac{3}{2}}-\frac{8}{x}-1 \\ =4x-6x^{\frac{1}{2}}-\frac{8}{x^2} \end{gathered}[/tex]At this point we should note that the slope (gradient) is the value of this first derivative when x = 4.
We can now plug in this value and we'll have;
[tex]\begin{gathered} f^{\prime}(x)=4x-6x^{\frac{1}{2}}-\frac{8}{x^2} \\ At\text{ } \\ x=4,\text{ we would have;} \\ f^{\prime}(4)=4(4)-6(4)^{\frac{1}{2}}-\frac{8}{4^2} \\ f^{\prime}(4)=16-6(2)-\frac{8}{16} \\ f^{\prime}(4)=16-12-\frac{1}{2} \\ f^{\prime}(4)=3\frac{1}{2} \\ OR \\ f^{\prime}(4)=\frac{7}{2} \end{gathered}[/tex]Now we can see the slope of the curve. The slope of the normal line perpendicular to the tangent of the curve is a negative inverse of this.
The negative inverse of 7/2 would be;
[tex]\begin{gathered} \text{Gradient}=\frac{7}{2} \\ \text{Gradient of perpendicular}=-\frac{2}{7} \end{gathered}[/tex]Now to use this value to derive the equation in the form
[tex]ax+by+c=0[/tex]We start by expresing this in the form;
[tex]y=mx+b[/tex]We now have;
[tex]y=-\frac{2x}{7}+b[/tex]We can convert this to the standard form as indicated earlier;
[tex]\begin{gathered} From\text{ the original equation; when} \\ x=4 \\ y=2(4)^2-4(4)^{\frac{3}{2}}-\frac{8}{4}-1 \\ y=32-4(8)-2-1 \\ y=32-32-2-1 \\ y=-3 \end{gathered}[/tex]With the points
[tex](4,-3)[/tex]We now have, the equation;
[tex]\begin{gathered} y=mx+b \\ -3=-\frac{2(4)}{7}+b \\ -3=-\frac{8}{7}+b \end{gathered}[/tex]We now collect like terms;
[tex]\begin{gathered} b=\frac{8}{7}-3 \\ b=-\frac{13}{7} \end{gathered}[/tex]We now have the y-intercept as calculated above.
We can now write up our equation is the standard form as indicated from the beginning;
[tex]\begin{gathered} ax+by+c=0 \\ (x,y)=(4,-3) \\ c=-\frac{13}{7} \end{gathered}[/tex][tex]\begin{gathered} 4a+(-3)b+(-\frac{13}{7})=0 \\ 4a-3b-\frac{13}{7}=0 \end{gathered}[/tex]Note that A, B and C must be integers. Therefore, we multiply all through by 7;
ANSWER:
[tex]28a-21b-13=0[/tex]For each angle θ listed below, find the reference angle α, and then find sin θ. Round sin θ to four decimal places, if necessary.θ = 255° ? ?
Answers
A reference angle is the angle created by the terminal arm and X-axis, and must be in the same quadrant as the terminal arm.
The given angle is 255°. It is located at quadrant III, then we can find the reference angle by subtracting 180°:
[tex]255\degree-180\degree=75\degree[/tex]The sin of 75 is:
[tex]\sin 75\degree=0.9659[/tex]In quadrant III, the sine is negative, then the sin of 255° is equal to the sine of 75° but negative. So:
[tex]\sin 255\degree=-0.9659[/tex]The answer is option C. sin75=0.9659 sin255=-0.9659
Answer:
The answer is option C. sin75=0.9659 sin255=-0.9659
Step-by-step explanation:
Given the equation of the function, write the equation of the inverse, g(x). f(x) = 3x -1
Answers
1. Replace f(x) with y:
y = 3x - 1
2. Replace every "x" with "y" and every "y" with "x":
x = 3y - 1
3. Solve for y:
Add 1 to both sides:
x + 1 = 3y -1 + 1
x + 1 = 3y
Divide both sides by 3:
(x + 1)/3 = 3y/3
y = (x + 1)/3
4. Replace y with f−1(x) :
f-1 (x) = (x + 1)/3
Choose the point-slope form of the equation below that represents the line that passes through the points (-6, 4) and (2.0), (2 points)Oy - 4 = 2(x + 6)O y + 6 = 2(x - 4)Oy+6=-= (x-4)Oy-4--3(x+6)
Answers
Given the following:
(-6, 4) and (2, 0) are the lines that passes through the point.
we are asked to choose the point slope equation.
before we can solve it, we must first of all solve for the slope.
Slope m = y2 - y1
x2 - x1
where:
x1 = -6
x2 = 2
y1 = 4
y2 = 0
m = 0 - 4
2 - (-6)
m = -4/8
m = -1/2
The equation of the lines is found using the point-slope form:
y - y1 = m(x - x1)
so lets substitute into the above equation:
recall, y1 = 4, x1 = -6, slope m = -1/2
y - 4 = -1/2(x - (-6))
y - 4 = -1/2(x + 6)
Therefore, the equation of the lines using the point-slope form is:
y - 4 = -1/2(x + 6)
so the correct option is D which is y - 4 = -1/2(x + 6)
Select the quadrant or axis where each ordered pair is located on a coordinate plane.(9.5, 0)(-4, 7)(-1, -8)options:Quadrant IQuadrant IIQuadrant IIIQuadrant IV
Answers
The points (9.5, 0), (-4, 7), and (-1, -8) are plotted in the coordinate plane below:
Therefore, the quadrants where each point is located are:
• Quadrant I: (9.5, 0)
,• Quadrant III: (-1, -8)
,• Quadrant IV: (-4, 7)
Lin is solving the inequality 15-x< 14. She knows the solution to the equation 15 - x = 14 is x = 1 How can Lin determine whether x > Torx < 1 is the solution to the inequality?
Answers
The inequality we have is:
[tex]15-x<14[/tex]To solve this problem the x has to be positive, for this reason, the first step is to add x to both sides of the inequality:
[tex]15-x+x<14+x[/tex]As you can see, on the left side -x+x is equal to 0. So we have:
[tex]15<14+x[/tex]The next step to solving for x, now that the x is positive, is to leave the term with x alone on one side of the inequality. For this reason, we need to subtract 14 to both sides of the inequality:
[tex]15-14<14-14+x[/tex]On the right side, 14-14 is equal to 0, and thus we will be left only with "x" on that side:
[tex]15-14On the left side, 15-14 is equal to 1:[tex]1This can be read as follows: "x is greater than 1".And we can also write this solution with the x at the beginning:
[tex]x>1[/tex]Answer: x>1
The terminal side contains the point (-6, -8). Find tan θ.Question 18 options:.751.3-.75-1.3
Answers
Given:
The terminal side contains the point (-6, -8).
To find:
[tex]\tan \theta[/tex]Here, x= -6 and y= -8.
Using the formula,
[tex]\begin{gathered} \tan \theta=\frac{y}{x} \\ \tan \theta=\frac{-8}{-6} \\ \tan \theta=1.3 \end{gathered}[/tex]Hence, the answer is,
[tex]1.3[/tex]In the given diagram, line segment BDbisects angle ABC. Segment BDis extended to E, where line segment ECis parallel to line segment AB.Write a two-column proof to show that AB/AD=BC/DC
Answers
Explanation:
From the question , we will utilize the concept of isosceles triangles
Concept:
The isosceles triangle theorem states that the angles opposite to the equal sides of an isosceles triangle are equal in measurement. So, in an isosceles triangle △ABC where AB = AC, we have ∠B = ∠C.
From the steps, we can see that
[tex]\angle2\cong\angle5(substituting\text{ property of congruency\rparen}[/tex]Hence,
We can cconclude that the final answer is
[tex]EC=BC(properties\text{ of isosceles triangles\rparen}[/tex]
OPTION A is the correct answer
Answer:
EC = BC; property of isosceles triangle
Hope this helps!
Step-by-step explanation:
How do you perform the indicated operation?(4y + 11)(3y² -2y -7)
Answers
we use distributive property
[tex](4y\times3y^2)+(4y\times-2y)+(4y\times-7)+(11\times3y^2)+(11\times-2y)+(11\times-7)[/tex][tex]\begin{gathered} (12y^3)+(-8y^2)+(-28y)+(33y^2)+(-22y)+(-77) \\ 12y^3-8y^2+33y^2-28y-22y-77 \\ 12y^3+25y^2-50y-77 \end{gathered}[/tex]School is making digital backups of old reels of film in its library archives the table shown approximate run Times of the films for a given diameter of film in the reel. Which of the following equations is a good model for the run time, y, as a function of the diameter, X?
Answers
One technique that you can apply when solving such a problem is trial and error. We try to use each equation to prove that a given value of x on the table given will correspond to the value of y on the table.
a) Let's try to put x = 3 for the first equation and we must get an answer equal to 2.25.
[tex]y=7.72(3)-29.02=-5.86_{}[/tex]Since the value of y is not equal to 2.25 and the deviation is too large. this equation is not a good model,
b) We put x = 3 on the second equation and solve for y
[tex]y=-7.52(3)^2+0.19(3)+3.26=-63.85[/tex]Since the value of y is not equal to 2.25 and the deviation is too large. this equation is not a good model,
c) We put x = 3 on the third equation and solve for y,
[tex]y=0.4(3)^2+0.79(3)-4.93=1.04[/tex]Again, the value that we get is not equal to 2.25, hence, this equation is not a good model. But since its value is close to 2.25, we try to other values of x. If x = 5, we get
[tex]y=0.4(5)^2+0.79(5)-4.93=9.02[/tex]which has a slight deviation on the given value of y on the table for x = 5. let's try for x = 7. We have
[tex]y=0.4(7)^2+0.79(7)-4.93=20.2[/tex]and the answer has a small deviation compared to the actual value given. The other values of x can again be put on the equation and check their corresponding value of y, and the resulting values are as follows
[tex]\begin{gathered} y=0.4(8)^2+0.79(8)-4.93=26.99 \\ y=0.4(12)^2+0.79(12)-4.93=62.15 \\ y=0.4(14)^2+0.79(14)-4.93=84.53 \end{gathered}[/tex]And as you can see, the deviation of values from the table to calculated becomes smaller. Hence, this is the best model.
d) We put x = 3 on the third equation and solve for y,
[tex]y=4.19(1.02)^3=4.45_{}_{}[/tex]Again, the value that we get is not equal to 2.25, hence, this equation is not a good model. But since its value is close to 2.25, we try to other values of x. If x = 5, we get
[tex]y=4.19(1.02)^5=4.63[/tex]where the answer's deviation is too large compared to the value of y if x = 5 on the table given.
Based on the calculations used above, the best equation that can be a good model is equation 3.
Use the approximate half-life formula for the case described below. Discuss whether the formula is valid for the case described.Urban encroachment is causing the area of a forest to decline at the rate of 9% per year. What is the half-life of the forest? What fraction of the forest will remain in 30 years?(Type an integer or decimal rounded to the nearest hundredth as needed.)
Answers
Answer:
Half-life = 7.35 years
After 30 years 0.06 of the forest will remain
Explanation:
Half-life is the amount of time it takes the forest to decline to half its initial value.
Now we are told that the forest declines at a rate of 9% per year. This means the amount left next year is 100% - 9% = 91% of the previous. Therefore, if we call the initial amount A, then the amount left after t years will be
[tex]P(t)=A(\frac{91\%}{100\%})^t[/tex][tex]\Rightarrow P(t)=A(0.91)^t[/tex]Now, when the forest declines to half its initial value, we have
[tex]\frac{A}{2}=A(0.91)^t[/tex]Canceling A from both sides gives
[tex]\frac{1}{2}=0.91^t[/tex]Taking the logarithm (of base 0.91) of both sides gives
[tex]\log_{0.91}(\frac{1}{2})=t[/tex][tex]t=7.35\text{ years.}[/tex]The figure shows the first three in a sequence of squares. The first square in the sequence has a side length of 3 units, and each square after that has a side length that is 2 units longer than the previous square.What is the explicit equation for f (n) that represents the areas of the squares in the sequence? f (n) = 2(n − 1)2 + 3 f (n) = (3 + 2(n − 1))2 f (n) = (3 + 2n)2 f (n) = 3n2
Answers
SOLUTION:
Since the sequence of side lengths are;
[tex]3,3+2n,3+4n,...[/tex]Their areas would be the sequence;
[tex]9,(3+2n)^2,(3+4n)^2,...[/tex]Thus, the explicit formula for the area is;
[tex]f(n)=(3+2(n-1))^2[/tex]f (n) = (3 + 2(n − 1))² is the explicit equation for f (n) that represents the areas of the squares in the sequence
What is Sequence?a sequence is an enumerated collection of objects in which repetitions are allowed and order matters.
Given,
The figure shows the first three in a sequence of squares.
First three in a sequence of squares. The first square in the sequence has a side length of 3 units
Each square after that has a side length that is 2 units longer than the previous square.
3,3+2n,3+4n....
The area of square is square of its length
The areas would be the sequence
3²,(3+2n)²,(3+4n)²....
Thus, the explicit formula for the area is;
f (n) = (3 + 2(n − 1))²
Hence f (n) = (3 + 2(n − 1))² is the explicit equation for f (n) that represents the areas of the squares in the sequence
To learn more on Sequence click:
https://brainly.com/question/21961097
#SPJ2
Can you please help me out with a question
Answers
The arc length formula is:
[tex]L=\frac{\theta}{360}\cdot2\pi r[/tex]Where
θ is the angle
r is the radius
Given,
θ = 75°
r = 15
Now, we find the arc length (L) of Arc AC by substituting the information we know [ Remembering to use 3.14159 as π ]:
[tex]\begin{gathered} L=\frac{\theta}{360}\cdot2\pi r \\ L=\frac{75}{360}\cdot2(3.14159)(15) \\ L=\frac{5}{24}\cdot94.2477 \\ L=19.6349 \end{gathered}[/tex]Rounding to the nearest thousandth (3 decimal places), we have:
Arc Length = 19.635 unitsCan someone Help me with Trigonometry, will mark Brainliest if correct ;) show your work and draw a diagram of the answer pls
Answers
So we will use trigonometry to solve this because it is a right triangle. The hypotenuse is the ladder (h) and the two smallest sides are the floor and the vertical wall (w).
That angular ladder does with the ground= A
sin A = opposite / hypotenuse
[tex]\begin{gathered} \sin \text{ A = }\frac{14.8}{15}=0.986 \\ A=\sin ^{-1}(0.986)=80.4\text{degrees} \end{gathered}[/tex]No, the ladder will not be safe
Now let's make it safe:
The lenght of the ladder (w) is constant, so it remains 15
So now let's ask in an inequality what height will be safe (70degrees or less)
[tex]\begin{gathered} A=\sin ^{-1}(\frac{w}{15})\leq70 \\ \sin (\sin ^{-1}(\frac{w}{15}))\leq\sin (70) \\ \frac{w}{15}\leq0.9396 \\ (15)\frac{w}{15}\leq0.9396(15) \\ w\leq14.09 \end{gathered}[/tex]What does that mean? As long as you position the ladder against the wall so that the height from the ground to the top of the ladder is <14.09 ft
At KEY Middle School, there are 240 girls and 160 boys. What percent of all the students are girls?
Answers
Given;
Number of boys = 160
Number of girls = 240
Total number of students = 160 + 240 = 400
To find the percentage of all students that are girls, use the formula below:
[tex]\begin{gathered} \text{ \% of girls = }\frac{Number\text{ of girls}}{Total\text{ number}}\times\frac{100}{1} \\ \\ \text{ } \end{gathered}[/tex]Therefore, we have:
[tex]\begin{gathered} \text{ \% of girls = }\frac{240}{400}\times\frac{100}{1} \\ \\ \text{ = }0.6\text{ }\times\text{ 100 = 60\%} \end{gathered}[/tex]The percent of all the students that are girls is 60 percent.
ANSWER:
60%
240/400 x 100/1
0.6 x 100 is 60
60%
The volume of the cylinder is approximately 7,959.9 cubic inches. The radius is ___ inches.Use π = 3.14.
Answers
The figure given is a cylinder.
The volume of a cylinder is given by the formula:
[tex]V=\pi r^2h[/tex]From the data given
The height is given to be 15 inches
The volume is also given to be 7,959.9 cubic inches
pi is 3.14
Upon substituting the values into the equation to solve for r, we will obtain
[tex]\begin{gathered} 7959.9=3.14\times r^2\times15 \\ 7959.9=47.1r^2 \end{gathered}[/tex][tex]\frac{47.1r^2}{47.1}=\frac{7959.9}{47.1}[/tex][tex]r^2=169[/tex][tex]\begin{gathered} r=\sqrt[]{169} \\ r=13\text{ inches} \end{gathered}[/tex]Radius is 13 inches
Which expression can be used to name the angle below?AE"There are 3 possible answersO ZUAEOZAO ZUEAZUNo answer text provided,ZEAUO ZAUE
Answers
An angle can be named in several ways:
*With the capital letter representing its vertex
*With three capital letters: the two extreme letters represent the sides and the middle one the vertex.
In the figure you can see that the vertex of the angle is A and that the sides are E and U, then, the expressions you can use to name the shown angle are:
[tex]\begin{gathered} \angle A \\ \angle EAU \\ \angle UAE \end{gathered}[/tex]One custodian cleans a suite of offices in 8 hours. When a second worker is asked to join the regular custodian, the job takes only 4 hours. How long does it take thesecond worker to do the same job alone?The second worker can do the same job alone in___hours.
Answers
Given:
One custodian cleans a suite of offices in 8 hours.
So, the rate of the custodian to clean the office = 1/8
When a second worker is asked to join the regular custodian, the job takes only 4 hours.
So, the rate of both custodians = 1/4
Let the rate of the second custodian = x
So,
[tex]\frac{1}{8}+x=\frac{1}{4}[/tex]Solve for x:
[tex]x=\frac{1}{4}-\frac{1}{8}=\frac{1}{8}[/tex]So, the rate of the second custodian = 1/8
This means he will take 8 hours to clean the office alone
So, the answer will be:
The second worker can do the same job alone in 8 hours.
What is the length, in whole meters, of the plastic edging that Amy needs to complete this project?
Answers
The curved path edges are in a form of two pairs of quadrants. One pair is shown below:
We can find the lengths of the inner and outer arcs using the radii of 4m and 6m respectively.
The formula to find the length of the arc of a quadrant is
[tex]L=\frac{1}{2}\pi r[/tex]Length of inner arc:
[tex]\begin{gathered} l=\frac{1}{2}\times\pi\times4 \\ l=6.3m \end{gathered}[/tex]Length of outer arc:
[tex]\begin{gathered} L=\frac{1}{2}\times\pi\times6 \\ L=9.4m \end{gathered}[/tex]Hence, the length of the pair of arcs is
[tex]6.3+9.4=15.7m[/tex]For the two pairs, we have the length to be
[tex]\begin{gathered} 15.7\times2 \\ =31.4m \end{gathered}[/tex]Hence, it will take approximately 32 meters of plastic edging to complete the project.
NEED HELP!! Graph each function.Find the asymptote. Tell how the graph is transformedfrom the graph of its parentfunction.2. f(x)=3log4 (x + 6)1.f(x)= log₂x +43.f(x)=log (x+5)5.f(x)=2.5log2 (x+7)-34. f(x) = 3 + ln x6. f(x)=-0.8 In (x-1.5) +2
Answers
1)
The given function is expressed as
f(x) = log2x + 4
where
2 is the base of the logarithm
The graph is shown below
If a function, f(x) is translated d units upwards, it becomes f(x) + d
For the given function, the parent function is f(x) = log2x where 2 is the base.
f(x) = log2x + 4 means that the parent function was translated or shifted by 4 units upwards
On the left, the graph gets close to x = 0 but it doesn't touch it. Thus,
Vertical asymptote is x = 0
Set m to 0.0 to create a horizontal line. Then set x, to 3.0 and y, to -2.0.
Answers
We have the following:
the equation in the slope form is:
[tex]y=mx+b[/tex]m = 0 and goes through (3, -2)
therefore:
[tex]\begin{gathered} -2=3\cdot0+b \\ b=-2 \end{gathered}[/tex]now,
[tex]\begin{gathered} m=0 \\ \text{point = (3,-2)} \\ y=-2 \end{gathered}[/tex]Answer 23 and the 24 ples explain. draw the problem or calculate it.
Answers
Given :
The slope = -3
Y- intercept = 7
The general equation of the line is :
[tex]y=m\cdot x+b[/tex]Where m is the slope and b is y- intercept
So,
[tex]\begin{gathered} m=-3 \\ b=7 \end{gathered}[/tex]Substitute with m and b in the general form
so, the equation of the line will be :
[tex]y=-3x+7[/tex]
Vector u has initial point at (8, 6) and terminal point at (–6, 12). Which are the magnitude and direction of u?
Answers
SOLUTION
Write out the given point
[tex](8,6)\text{ and (-6,12)}[/tex]The magnitude of the vertor u is the distance between the two point.
[tex]\begin{gathered} \text{distance = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{Where } \\ x_2=-6,x_1=8 \\ y_2=12,y_1=6 \end{gathered}[/tex]Substitute into the formula, we have
[tex]\begin{gathered} \mleft\Vert u\mleft\Vert=\sqrt[]{(-6-8)^2+(12-6)^2}\mright?\mright? \\ \mleft\Vert u\mleft\Vert=\sqrt[]{(-14)^2+6^2}\mright?\mright? \\ \mleft\Vert u\mleft\Vert=\sqrt[]{169+36}=\sqrt[]{232}\mright?\mright? \end{gathered}[/tex]Hence
|| u || =15.23
The magnitude of the vector is 15.232
Then the direction is obtain by using the formula
[tex]\begin{gathered} \tan \theta=\frac{y_2-y_1}{x_2-x_1} \\ \text{Then } \\ \tan \theta=\frac{12-6}{-6-8}=\frac{6}{-14}=-0.4286 \end{gathered}[/tex]Then we have
[tex]\tan \theta=-0.4286[/tex]take inverse tan of the equation above, we have
[tex]\begin{gathered} \theta=\tan ^{-1}(-0.4286) \\ \theta=156.801^0 \end{gathered}[/tex]Hence
The direction is of u is 156.801°
Answer: Second Option
what is the inequality of 7x ≤14 on a numberline
Answers
To find the inequality on a number line, we need to solve the inequality for x:
[tex]7x\leq14[/tex]Divide both sides by 7 to isolate the x variable:
[tex]\frac{7x}{7}\leq\frac{14}{7}[/tex][tex]x\leq\frac{14}{7}[/tex]Then:
[tex]x\leq2[/tex]Therefore, the inequality represents that x can be equal to or less than 2
I need help graphing a problem I have the answer I just need help learning to graph
Answers
Given the inequality:
[tex]\frac{a}{10}-6>-12[/tex]Solving the inequality as follows:
Multiply both sides by 10
[tex]\begin{gathered} 10\cdot\frac{a}{10}-10\cdot6>10\cdot(-12) \\ a-60>-120 \end{gathered}[/tex]Add (60) to both sides:
[tex]\begin{gathered} a-60+60>-120+60 \\ a>-60 \end{gathered}[/tex]The solution on the number line will be as follows:
Solve the following equation for "b".b/3 = M
Answers
In order to solve an equation for a variable we need to isolate it on the left side. In this case we want to find the value of "b", therefore we must perform operations in such a way that it will be the only thing on the left side of the equation. To do so we need to switch the operation of each term we don't want to be on the left side, this means that if a term is adding it should go to the right side subtracting and if it is multiplying it should go dividing. In this case there is only one term that is dividing "b", so it should go to the right side by multiplying. With this in mind lets solve the problem:
[tex]\begin{gathered} \frac{b}{3}\text{ = M} \\ b\text{ = 3}\cdot M \end{gathered}[/tex]Suppose an auto racer won a 400 mile race with a time of 1:48:51. At one point the racer was 50 miles closer to the finish than the start. How far had the racer gone at that point?How far from the start was the racer? __ miles
Answers
To solve this problem, let's use the variables x and y to represent the distance of the racer to the start and to the finish, respectively.
If the total distance of the race is 400 miles, we have that the distance traveled by the racer until now (x) plus the distance he needs to travel to finish the race (y) is 400:
[tex]x+y=400[/tex]Also, at one point the racer was 50 miles closer to the finish than the start, so at that point we have that he is farther away from the beginning (that is, x is 50 units bigger than y):
[tex]x=y+50[/tex]Now, using this value of x in the first equation, we have:
[tex]\begin{gathered} (y+50)+y=400 \\ 2y+50=400 \\ 2y=350 \\ y=\frac{350}{2}=175 \end{gathered}[/tex]Now, finding the value of x, we have:
[tex]x=y+50\to x=175+50\to x=225[/tex]So the racer was 225 miles far from the start.
A doctor conducts an experiment to test new treatments for a medical condition. Out of the 6 volunteers in the experiment, 4 do not receive any treatment. What percent of the volunteers do not receive any treatment?
Answers
ANSWER
66.67%
EXPLANATION
We have that there were 6 volunteers in the experiment and 4 do not receive any treatment.
To find the percent of volunteers that do not receive any treatment, we have to divide the number of people that do not receive treatment by the total number of people that were in the experiment and multiply by 100.
That is:
[tex]\frac{4}{6}\cdot\text{ 100 = 66.67\%}[/tex]That is the percent of volunteers that do not receive any treatment.
Solve the following equation on the interval [0°, 360º). Round answers to the nearest tenth. If there is no solution, indicate "No Solution."2sec^2(x) - 13tan(x) = -13
Answers
Given
[tex]2\sec ^2(x)-13\tan (x)=-13[/tex]Add 13 to both sides
[tex]\begin{gathered} 2\sec ^2(x)-13\tan (x)+13=-13+13 \\ 2\sec ^2(x)-13\tan (x)+13=0 \end{gathered}[/tex]We have that
[tex]\sec ^2(x)=1+\tan ^2(x)[/tex]So, substitute in the above equation
[tex]2(1+\tan ^2(x))-13\tan (x)+13=0[/tex]Simplify
[tex]\begin{gathered} 2+2\tan ^2(x)-13\tan (x)+13=0 \\ 15+2\tan ^2(x)-13\tan (x)=0 \end{gathered}[/tex]Reordering the equation
[tex]2\tan ^2(x)-13\tan (x)+15=0[/tex]We get a quadratic equation, then solve by factoring
[tex](2\tan (x)-3)(\tan (x)-5)=0[/tex]Separate the solutions
[tex]\begin{gathered} 2\tan (x)-3=0 \\ 2\tan (x)-3+3=0+3 \\ 2\tan (x)=3 \\ \frac{2\tan (x)}{2}=\frac{3}{2} \\ \tan (x)=\frac{3}{2} \end{gathered}[/tex]And
[tex]\begin{gathered} \tan (x)-5=0 \\ \tan (x)-5+5=0+5 \\ \tan (x)=5 \end{gathered}[/tex]Next, solve for x for each solution
[tex]\begin{gathered} \tan (x)=\frac{3}{2} \\ x=\tan ^{-1}(\frac{3}{2}) \\ x=56.3 \end{gathered}[/tex]And
[tex]\begin{gathered} \tan (x)=5 \\ x=\tan ^{-1}(5) \\ x=78.7 \end{gathered}[/tex]Answer:
x = 56.3° and x = 78.7°
Find the equation for the line that passes through the point (2,4) and that is parallel to the line with the equation x=-2
Answers
Given:
The passing point of line is (2,4)
The line is parallel to x = - 2
Any equation parallel to x= A has an equation of the form x = B.
Now the equation passing through (2,4) and parallel to x = - 2 is given by :
[tex]x=2[/tex]This is the required answer.